Как решать примеры со скобками

С порядком выполнения действий в математических примерах часто возникает путаница. Ситуация осложняется, когда появляются скобки, которые могут не просто разделять длинное выражение на отдельные части, но и менять порядок действий.

«Бери и Делай» собрал в одной статье все, о чем нужно помнить, когда вы решаете примеры со скобками.

Порядок выполнения действий в выражениях без скобок

Для решения простых примеров без скобок, вычисления корней и дробей достаточно запомнить правила:

• Все действия выполняются по порядку слева направо.
• Сначала выполняются действия умножения и деления, а затем — сложения и вычитания.

Как это применяется на практике?

Пример № 1. Вычислите: 15 − 3 + 7.

Сначала выполняем все действия по порядку слева направо:

1) 15 − 3 = 12

2) 12 + 7 = 19

Получаем ответ: 15 − 3 + 7 = 19.

Пример № 2. Вычислите: 10 ÷ 2 × 8.

Здесь тоже выполняем все действия по порядку слева направо:

1) 10 ÷ 2 = 5

2) 5 × 8 = 40

Получаем ответ: 10 ÷ 2 × 8 = 40.

Пример № 3. Вычислите: 5 × 4 − 8 ÷ 2.

Здесь тоже двигаемся слева направо, но держим в уме правило о том, что умножение и деление необходимо выполнить в первую очередь. Поэтому действуем так:

1) 5 × 4 = 20. Это умножение, и оно стоит на первом месте, если двигаться слева направо.

2) 8 ÷ 2 = 4. Это деление, и у него есть приоритет перед действием вычитания, поэтому, несмотря на то, что оно находится правее, из-за приоритета мы выполняем его сразу после умножения.

3) 20 − 4 = 16. Здесь по порядку: выполнив умножение и деление, переходим к вычитанию.

Получаем ответ: 5 × 4 − 8 ÷ 2 = 16.

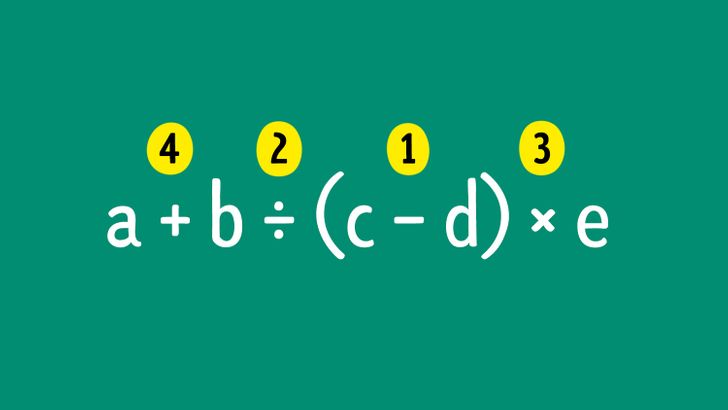
Если выражение состоит из нескольких действий или вы только учите их порядок, можно над знаками арифметических действий проставлять числа, подсказывающие порядок выполнения вычислений, как на картинке выше.

Важно: Скобки не нужно ставить, если действия сложения и вычитания выполняются в последовательности слева направо. К примеру, вместо (4 − 2) + 3 достаточно написать просто 4 − 2 + 3. Также нет необходимости добавлять скобки, чтобы выделить действия, которые и так имеют приоритет. К примеру, вместо 5 + (4 × 3) достаточно написать лишь 5 + 4 × 3, так как в этом случае действие умножения и без скобок имеет приоритет перед действием сложения.

Порядок выполнения действий в выражениях со скобками

Выражение может содержать скобки, задача которых — изменить привычный порядок выполнения математических действий. Чтобы не запутаться, запомните следующие правила:

• Сначала нужно выполнить действия в скобках.
• Затем все остальные по порядку, двигаясь слева направо.
• При этом сначала выполняются действия умножения и деления, а после — сложения и вычитания.
• Внутри скобок действует аналогичный порядок.
• Если в выражении есть дроби или степени, по возможности их следует вычислить до того, как вы перейдете к умножению и делению, а затем сложению и вычитанию.

Как это применяется на практике?

Пример № 1. Вычислите: 5 × (8 − 4) ÷ 2.

Следуя вышеуказанным правилам, сначала выполним действие в скобках, а затем по порядку все остальные. Тогда получается:

1) 8 − 4 = 4

Зная результат действия в скобках, в черновике для удобства мы можем записать выражение как 5 × (8 − 4) ÷ 2 = 5 × 4 ÷ 2. Теперь по порядку выполним действия умножения и деления:

2) 5 × 4 = 20

3) 20 ÷ 2 = 10

Получаем, что 5 × (8 − 4) ÷ 2 = 10.

Ответ: 5 × (8 − 4) ÷ 2 = 10.

Пример № 2. Вычислите и сравните результаты: 7 − 3 + 2 и 7 − (3 + 2).

Вычислим результат первого выражения: 7 − 3 + 2 = 6. Теперь посчитаем результат второго выражения: 7 − (3 + 2) = 7 − 5 = 2. Наличие скобок во втором примере изменило порядок действий, поэтому результаты двух выражений различаются.

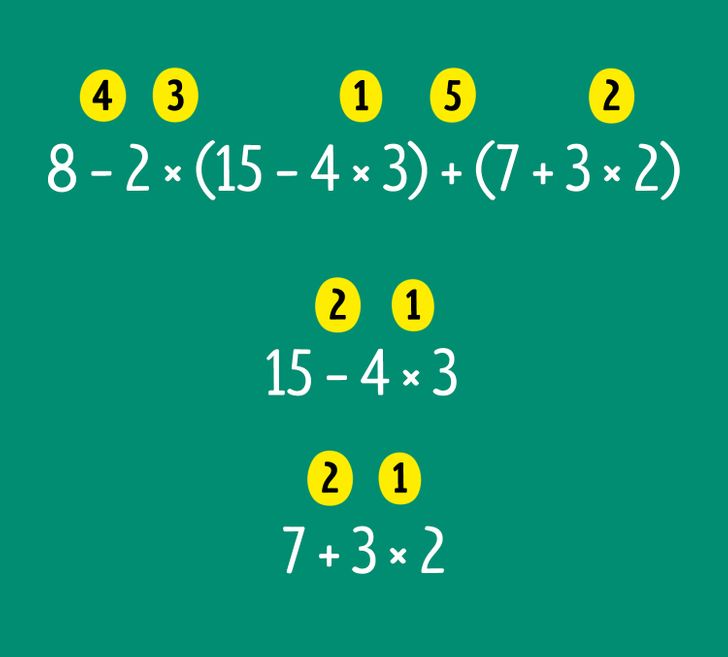
Пример № 3. Вычислите 8 − 2 × (15 − 4 × 3) + (7 + 3 × 2).

На первый взгляд, это выражение кажется сложным. Чтобы упростить процесс вычисления, разложите его на отдельные действия по порядку:

1) Сначала выполните действия в скобках. Чтобы получить результат выражения в первых скобках, нужно вспомнить о том, какие действия имеют приоритет. Таким образом, сначала вычисляем 4 × 3, затем результат вычитаем из числа 15. Получаем в ответе 3. Проделайте то же самое со вторыми скобками: вычислите 3 × 2 и к результату прибавьте 7. В ответе получаете 13.

2) Зная результаты вычислений в скобках, в черновике вы можете упростить выражение до вида: 8 − 2 × 3 + 13. Теперь нужно выполнить умножение, а затем по порядку вычитание и сложение: 8 − 6 + 13 = 2 +13 = 15. Получаем ответ: 8 − 2 × (15 − 4 × 3) + (7 + 3 × 2) = 15.

Важно: Можно встретить выражения, где в одних скобках содержатся другие скобки. В этом случае действия аналогичные: сначала надо вычислить результат выражения во внутренних скобках, затем работать с внешними и в конце перейти к тому, что находится вне скобок. Кроме того, вид скобок может различаться: чаще всего это ( ), но допускается также использование { } и [ ].

Распространенные ошибки, из-за которых большинство неверно решают примеры со скобками

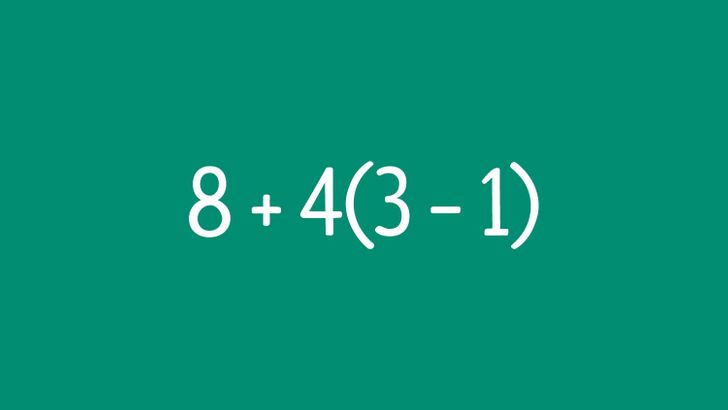
• Знак умножения опускается перед скобкой, из-за чего можно перепутать порядок действий

К примеру, нужно вычислить, чему равно выражение 8 + 4(3 − 1). Решая этот пример, можно по ошибке сначала посчитать результат вычитания в скобках, затем результат сложения, после чего перемножить полученные числа. Правильный порядок иной: сначала получаем результат вычитания в скобках, затем умножаем его на 4, после чего прибавляем полученное число к 8. Получается следующее: 8 + 4(3 − 1) = 8 + 4 × (3 − 1) = 8 + 4 × 2 = 8 + 8 = 16.

Чуть сложнее может выглядеть вот такое выражение: 8 ÷ 4(3 − 1). Здесь алгоритм действий аналогичный. Сначала выполняем действия в скобках, затем по порядку слева направо нужно выполнить деление и умножение: 8 ÷ 4 × (3 − 1) = 8 ÷ 4 × 2 = 2 × 2 = 4.

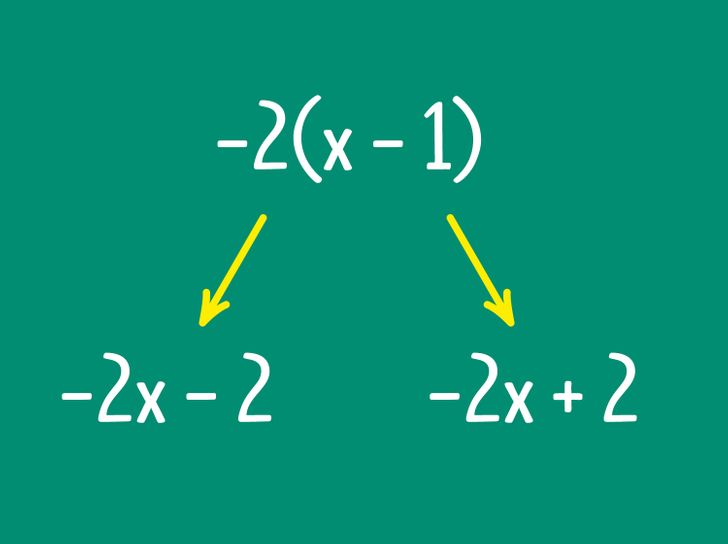
• Неправильно раскрыты скобки, перед которыми стоял минус

Бывают ситуации, когда скобки надо раскрыть, чтобы упростить выражение. В таком случае, если перед скобкой стоит минус, то при раскрытии скобки вместе с минусом опускаются, а знаки всех слагаемых, которые были внутри скобок, заменяются на противоположные, как если бы вы каждое число умножили на −1. К примеру, выражение 6 + 5 − (4 + 3 − 2) при раскрытии скобок превращается в 6 + 5 − 4 − 3 + 2. Чаще всего ошибки допускаются в выражениях, где есть переменные и много действий, к примеру: 3 + 2(x + 1) − 2(x − 1). Не зная значение переменной, мы не можем посчитать результат выражения в скобках, поэтому необходимо избавиться от скобок и упростить выражение до вида 3 + 2х + 2 − 2х + 2 = 7. Если скобки раскрыть неправильно, то можно получить 3 + 2х + 2 − 2х — 2 = 3.

• Вычисления производятся на калькуляторе

Далеко не все калькуляторы способны выполнить действия в правильном порядке, хотя есть модели, которые запрограммированы отделять простые операции от сложных вычислений в рамках одного выражения. Как проверить свой калькулятор? Попробуйте найти результат выражения 1 + 5 × 7. Если в ответе получилось 36, значит, калькулятор может решать сложные примеры, выполняя действия в правильном порядке.