Свойства степеней, которые пригодятся в жизни и школьникам, и их родителям

В жизни нередко возникают ситуации, когда полезно уметь правильно возводить число в степень, а также решать задачи, опираясь на особенности и свойства степеней. К примеру, без математических операций над числами в степени вы не сможете рассчитать, сколько плитки вам нужно приобрести, чтобы выложить пол и стены в ванной комнате.

«Бери и Делай» кратко объясняет, какими свойствами обладают степени и какие ошибки мы чаще всего допускаем, решая даже простые выражения с подобными числами. Сохраните эту статью, чтобы всегда иметь под рукой в нужный момент.

Что такое степень числа

Когда мы умножаем число само на себя, мы называем этот процесс возведением числа в степень. Так, если умножить число 3 само на себя, то мы запишем это как 3², или «три во второй степени».

Для 2-й и 3-й степеней часто используют специальные названия:

• возведение в квадрат (или возведение во 2-ю степень), например a²
• возведение в куб (или возведение в 3-ю степень), например a³

Если по известным значениям степени и показателя определяют неизвестное основание, это называется извлечением корня.

Свойства степеней

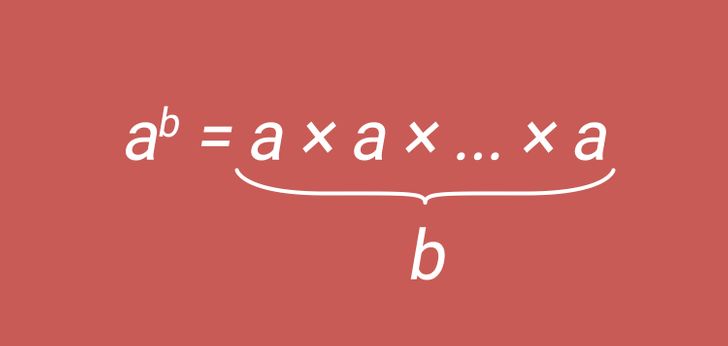
У степени есть основание и показатель. Посмотрите на картинку выше. Основание степени — это a, то есть повторяющийся множитель, а показатель степени — это b, то есть число, указывающее число повторений множителя. Читается это как «a в степени b».

Если показатель степени является натуральным числом, то его называют натуральным показателем. Из определения натуральных чисел следует, что натуральный показатель степени не может являться нулем, отрицательным или нецелым числом.

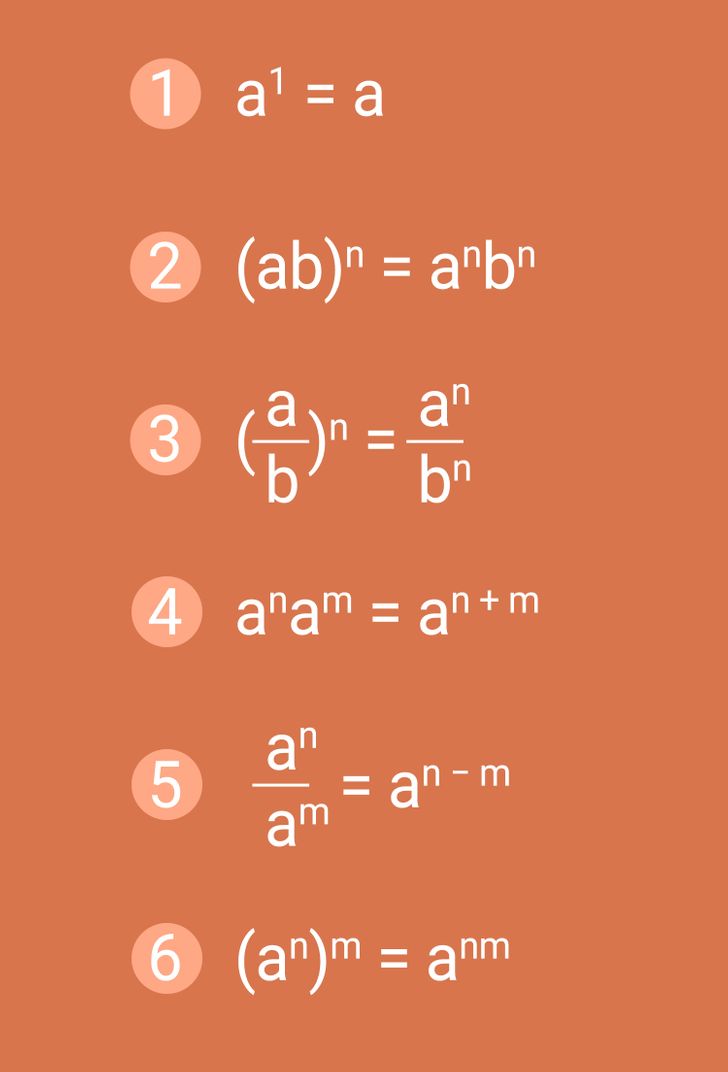
У степени с натуральным показателем есть несколько свойств, благодаря которым процесс вычислений можно упростить. Они перечислены выше. Давайте разберемся с каждым из них отдельно.

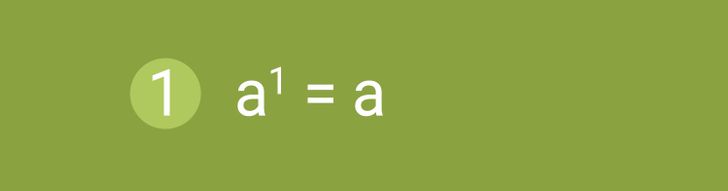
Свойство № 1: В 1-ю степень можно возвести любое число. И тогда число в 1-й степени будет равняться самому числу.

Например, 1¹ = 1, а 3¹ = 3. В алгебре 1-я степень обычно не записывается, но при действиях со степенями учитывается. Например, a⁴ × a = a⁴ × a¹ = a^{4 + 1} = a⁵.

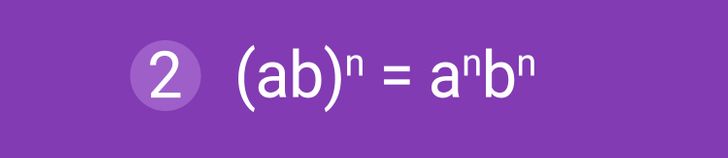
Свойство № 2: Степень произведения. Если нужно возвести в степень произведение множителей, то каждый из множителей возводят в степень, а затем результаты перемножают. При этом для вышеуказанной формулы важно, что a и b — это основания степеней (не равные нулю), а n — это показатель степени, натуральное число.

Пример использования: (3a)² = (3 × a)² = 3² × a² = 3²a².

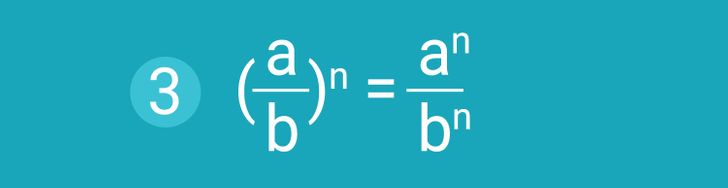
Свойство № 3: Степень частного. Если нужно возвести в степень результат деления делимого на делитель, то можно возвести в эту степень отдельно делимое и делитель, а затем первый результат разделить на второй. При этом для вышеуказанной формулы важно, что a и b — это основания степеней (не равные нулю) и любые рациональные числа, но b ≠ 0. А n — это натуральный показатель степени.

Пример использования: (5/8)² = 5² ÷ 8².

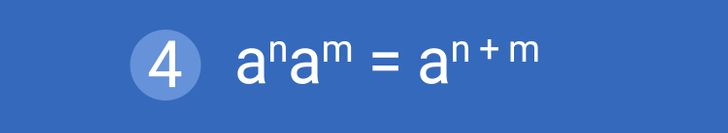
Свойство № 4: Произведение степеней. Если нужно умножить степени с одинаковыми основаниями, то основание оставляют без изменений, а показатели степеней складывают. При этом для вышеуказанной формулы важно, что n, m — это натуральные показатели степени.

Пример использования: 3⁴3⁵ = 3⁴ × 3⁵ = 3^{4 + 5} = 3⁹.

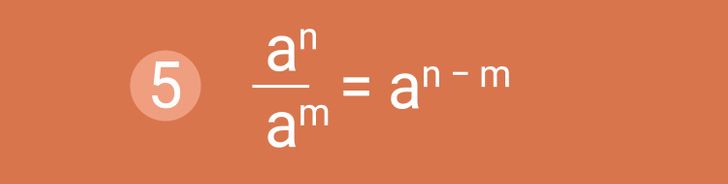
Свойство № 5: Частное степеней. Если нужно разделить степени с одинаковыми основаниями, то основание оставляют без изменений, а из показателя степени делимого вычитают показатель степени делителя. При этом для вышеуказанной формулы важно, что a — любое число, не равное нулю, a n, m — это любые натуральные числа, но такие, что n > m.

Пример использования: 4⁸ ÷ 4⁵ = 4^{8 − 5} = 4³.

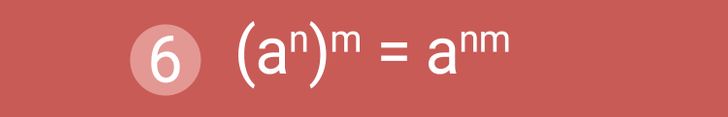
Свойство № 6: Возведение степени в квадрат. Если нужно возвести степень в степень, то основание степени оставляют без изменений, а показатели степеней умножают друг на друга. При этом для вышеуказанной формулы важно, что a — основание степени (не равное нулю), a n, m — натуральные показатели степени.

Пример использования: (4²)³ = 4^{2 × 3} = 4⁶.

Другие свойства степеней

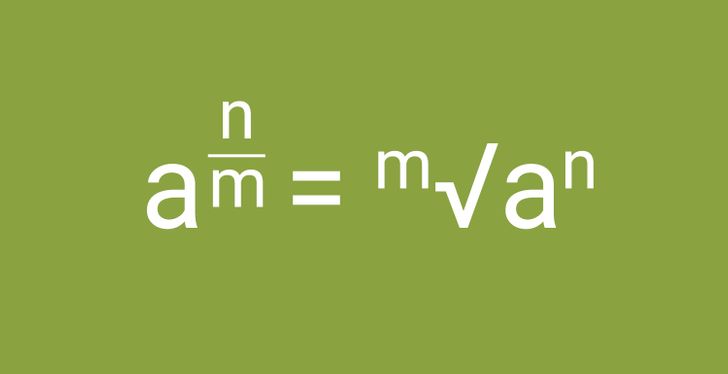
Число с дробным показателем степени равняется корню с показателем, равным знаменателю, и подкоренным числом в степени, равной числителю. Получается, что операцию извлечения корня всегда можно заменить возведением в степень. Это хорошо использовать для упрощения записи выражения.

Пример использования: ³√a⁶ = a^{6 ÷ 3} = a².

Любое число, возведенное в нулевую степень, будет равно единице (за исключением нуля). Нуль в нулевой степени не определен, поэтому подобное выражение не имеет смысла.

Пример использования: 7⁴ × 7⁻⁴ = 7^{4 + (−4)} = 7⁰ = 1.

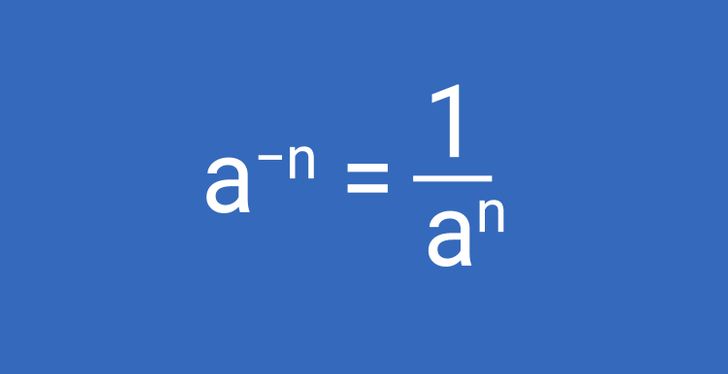
Любое число, возведенное в отрицательную степень, равно единице, разделенной на это же число, но в положительной степени. В частности:

• a⁻¹ = 1/a,
• (a/b)⁻ⁿ = (b/a)ⁿ

Пример использования: 6⁻² = 1/6² = 1/36.

Степень с отрицательным основанием и четным показателем равна степени с основанием, противоположным данному, но с тем же показателем. Чтобы возвести в нечетную степень отрицательное число, нужно поставить знак «минус» и возвести в эту степень число, противоположное данному.

Пример использования: (−8)⁴ = 8⁴ = 8 × 8 × 8 × 8 = 4 096. Или (−8)³ = −8³ = −512.

Какие ошибки часто допускают, когда речь идет о свойствах степеней

• Неправильно возводят число в нулевую, 1-ю и −1-ю степени, путая их между собой. Исходя из вышеуказанных свойств степеней, мы помним, что a⁰ = 1, a¹ = a, a⁻¹ = 1/a.

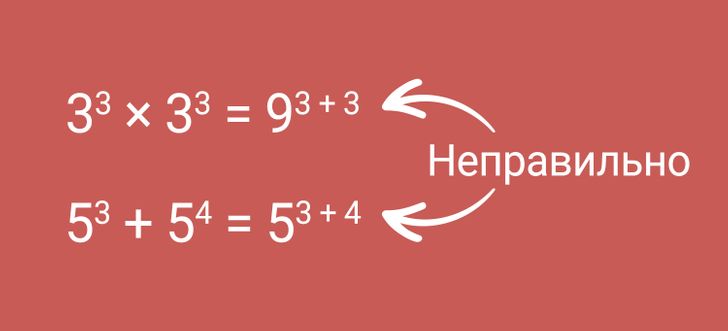
• Неправильно умножают и складывают степени. Чаще всего это происходит тогда, когда в выражении степени с одинаковыми основаниями. Посмотрите на картинку выше: в первом случае основания не перемножаются, то есть должно быть 3³ × 3³ = 3^{3 + 3} = 3⁶. А во втором случае при сложении мы не можем складывать показатели степени, даже если бы они были одинаковыми: нужно сначала возвести в степень каждое число, а затем произвести сложение, то есть 5³ + 5⁴ = 125 + 625 = 750.

• Неправильно возводят дробное число в отрицательную степень. На картинке выше только нижний вариант ответа соответствует правилу (a/b)⁻ⁿ = (b/a)ⁿ.

Бонус: проверьте себя, решив простой пример

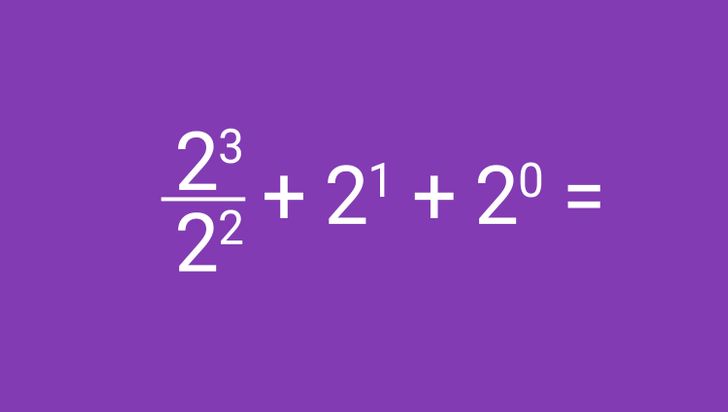
Этот пример выглядит настолько простым, что кажется, будто бы с ним мог бы справиться даже ребенок. Но на самом деле он легко поставит в тупик большинство взрослых. Главное здесь — это не попасть в ловушку и выполнить все действия в правильном порядке. Начнем с левой стороны и воспользуемся свойством частного степеней. Тогда 2³/2² = 2^{3 − 2} = 2¹. Далее подставим это число в выражение и получим 2¹ + 2¹ + 2⁰. На этом шаге кому-то захочется просто сложить показатели степеней. Но мы помним, что это неверный путь, и, воспользовавшись правилами возведения чисел в 1-ю и нулевую степени, получим 2¹ + 2¹ + 2⁰ = 2 + 2 + 1 = 5.

Ответ: 5.