Зачем нужны формулы сокращенного умножения

Умножение чисел не вызывает особых трудностей до тех пор, пока мы не сталкиваемся со сложными выражениями, где есть не только числа, но и переменные. Чтобы преобразовать или упростить такие выражения, можно использовать формулы сокращенного умножения. Они кажутся сложными, но лишь на первый взгляд.

«Бери и Делай» объясняет, что из себя представляют формулы сокращенного умножения, как их понять и использовать для решения разных задач.

Зачем нужны формулы сокращенного умножения

С этой темой чаще всего впервые сталкиваются в средней школе в рамках курса алгебры. На первый взгляд, все выглядит сложным, но формулы сокращенного умножения действительно помогают быстро и компактно произвести вычисления в определенных ситуациях.

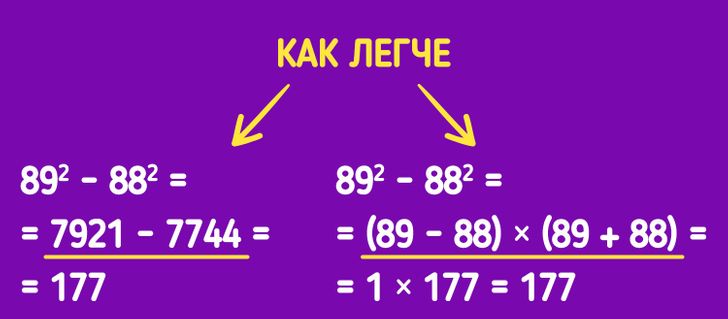
Ситуация № 1. Вы не хотите в уме возводить в степень большие числа, а затем производить математические действия с полученными результатами. Посмотрите на картинку выше: вместо того чтобы возводить числа 89 и 88 в квадрат, а затем заниматься вычитанием больших чисел, как это сделано на картинке слева, легче воспользоваться формулой разности двух квадратов a² − b² = (a − b) × (a + b), как это сделано на картинке справа.

Аналогично, чтобы возвести в квадрат большое число, можно воспользоваться формулой квадрата разности (a − b)² = a² − 2ab + b². Например: 79² = (80 − 1)² = 6400 − 160 + 1 = 6241.

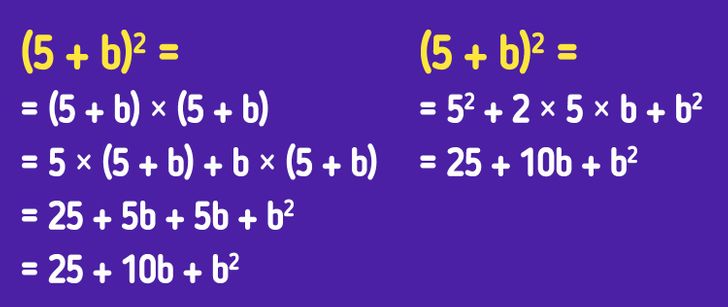
Ситуация № 2. Вы хотите избавиться от скобок в выражении, выполнив минимум действий. В примере выше для того, чтобы вынести из скобок выражение (5 + b)², справа мы воспользовались формулой квадрата суммы двух чисел (a + b)² = a² + 2ab + b², в результате получив выражение 25 + 10b + b². К этому же выражению можно прийти и без формулы, выполнив все действия последовательно, но именно благодаря формуле это быстрее и проще.

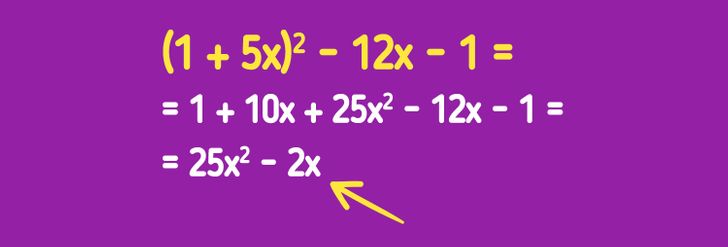
Ситуация № 3. Вам нужно привести многочлен (сумму произведений чисел и переменных) к стандартному виду. Для этого в примере на картинке выше мы снова использовали формулу квадрата суммы (a + b)² = a² + 2ab + b² и превратили (1 + 5x)² − 12x − 1 в 25ײ − 2x.

Какие бывают формулы сокращенного умножения

Математически доказать эти формулы несложно. Достаточно последовательно выполнить действия.

Пример № 1. Возьмем правую часть разности квадратов (a − b) × (a + b) и избавимся от скобок, получив (a − b) × (a + b) = a² + ab − ab − b². Так как ab − ab = 0, в итоге получаем, что (a − b) × (a + b) = a² − b².

Пример № 2. Возьмем правую часть формулы квадрата суммы (a + b)² и избавимся от степени, получив (a + b)² = (a + b) × (a + b). Уберем скобки, получив a² + ab + b² + ab, а затем a² + 2ab + b². В итоге получаем, что (a + b)² = a² + 2ab + b².

Пример № 3. Часто встречается формула квадрата суммы трех чисел, но что делать, если нам нужна формула квадрата разницы трех чисел? Попробуем ее получить самостоятельно:
(a − b − c)² = (a − b − c) × (a − b − c) = a² − ab − ac − ba + b² + bc − ca + cb + c² = a² − 2ab − 2ac + b² + 2bc + c². Для удобства восприятия ее можно записать так: (a − b − c)² = a² + b² + c² − 2ab − 2ac + 2bc.

Формулы для кубов доказать можно точно так же.

Пример № 1. Возьмем правую часть формулы разности кубов (a − b) × (a² + ab + b²) и избавимся от скобок, получив a³ + a²b + ab² − ba² − ab² − b³ = a³ + a²b − ba² − b³ = a³ − b³. В итоге получаем, что (a − b) × (a² + ab + b²) = a³ − b³.

Как запомнить формулы сокращенного умножения

В школе формулы сокращенного умножения учат наизусть. Если вы их случайно забудете, всегда можно с помощью нескольких действий привести выражение к упрощенному виду, как мы делали это выше в доказательствах. Но есть пара способов, которые могут облегчить запоминание.

Обычно сложнее всего запомнить коэффициенты и знаки в середине формулы, если речь идет об n-й степени суммы или разницы (квадрате суммы, квадрате разницы, кубе суммы, кубе разницы и так далее). Но можно их не запоминать, если на черновике рисовать небольшую подсказку — треугольник Паскаля.

Для начала на листке бумаге расположите три единицы: одна в середине, две другие у нее по бокам, но так, чтобы они все вместе образовывали треугольник.

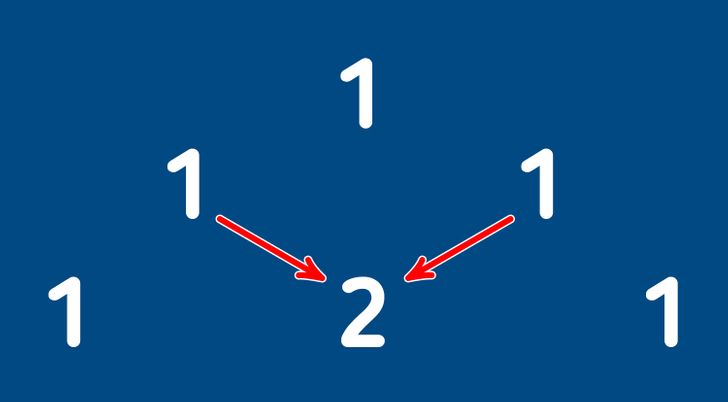
Строку с одной единицей будем считать нулевой. Таким образом, на первой строке располагаются две единицы. Чтобы получить вторую строчку, по краям снова расположим единицы, а между ними число, которое в сумме дают два вышестоящих над ним числа (единицы). Так в середине второй строчки появляется двойка.

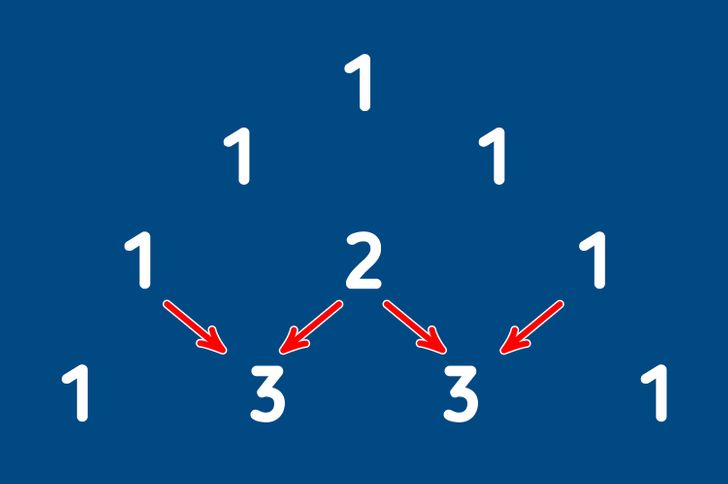
Теперь записываем третью строку. По краям ставим единицы (так будет всегда), затем между ними снова добавляем те числа, которые получаются в результате сложения вышестоящих, то есть тройки.

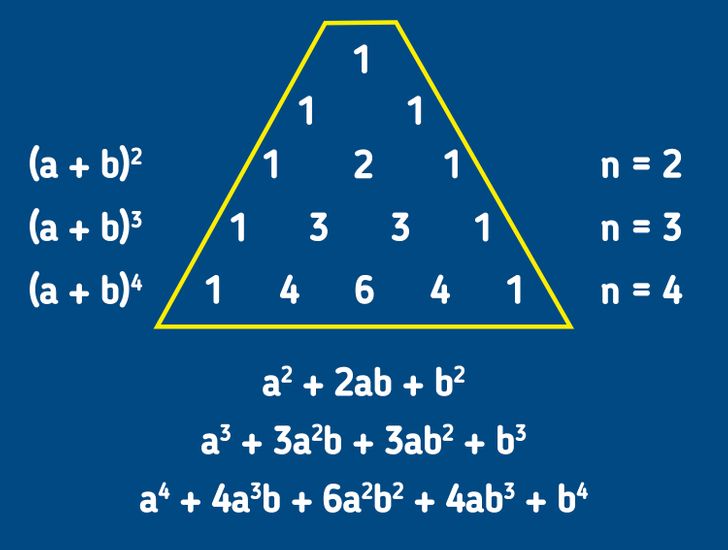
Продолжим заполнять таким образом треугольник до четвертой строчки. Что мы получили? Посмотрите на картинку выше. В каждой строке у нас коэффициенты из разложения двучлена в многочлен.

Теперь осталось разобраться со знаками. Как их запомнить? Первый из них будет таким же, как в раскладываемом двучлене (если раскладываем сумму, то это плюс, если разность — минус), а дальше знаки будут чередоваться.

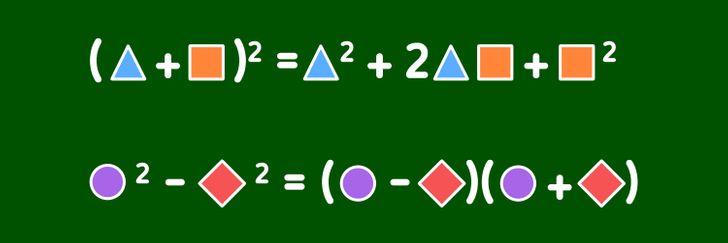
Альтернативный способ. Некоторым людям легче запомнить формулы, представляя вместо переменных абстрактные фигуры, как на изображении выше.

Как правильно читать формулы сокращенного умножения

• a² + b² = (a + b)² − 2ab

Сумма квадратов двух выражений равна разности квадрата суммы этих чисел и их удвоенного произведения.

• a² − b² = (a − b) × (a + b)

Разность квадратов двух выражений равна произведению их разности и их суммы.

• (a + b)² = a² + 2ab + b²

Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого на второе плюс квадрат второго выражения.

• (a − b)² = a² − 2ab + b²

Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого на второе плюс квадрат второго выражения.

• a³ + b³ = (a + b) × (a² − ab + b²)

Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.

• a³ − b³ = (a − b) × (a² + ab + b²)

Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.

• (a + b)³ = a³ + 3a²b + 3ab² + b³

Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго выражения.

• (a − b)³ = a³ − 3a²b + 3ab² − b³

Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго выражения.

Какие ошибки чаще всего допускают люди при использовании этих формул

• Путают сумму квадратов и квадрат суммы, разность квадратов и квадрат разности, сумму кубов и куб суммы, разность кубов и куб разности.

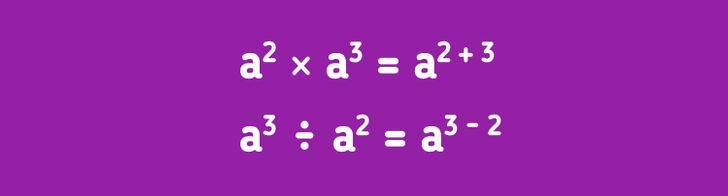
• Путают формулы сокращенного умножения и формулы умножения и деления переменных со степенями.

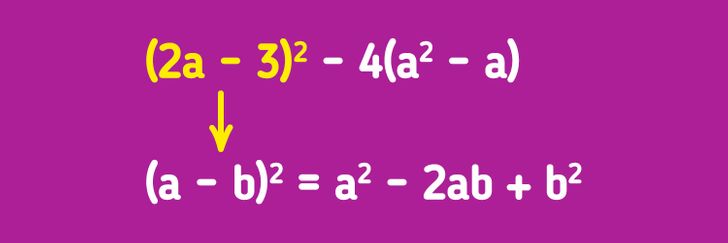
• Не замечают, что в выражении есть часть, которую можно упростить или решить с помощью формулы сокращенного умножения.

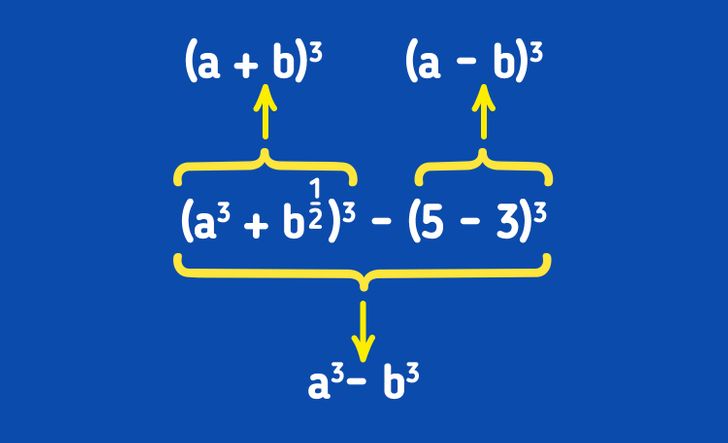
• Не видят формулу сокращенного умножения в выражении, потому что забывают, что иногда вместо одной переменной могут быть целые выражения.