Как решать задачи с закономерностями

Нас повсюду окружают различные типы математических закономерностей. К примеру, неделя состоит из 7 дней, и через 7 календарных дней наступит тот же день недели, что и сегодня. Это пример закономерности, которая имеет свойство повторяться. Зная, какая закономерность задает порядок между элементами, можно прогнозировать события. Поэтому тема математических закономерностей и задач с ними хотя и кажется простой, но является важной для изучения и понимания более сложных вещей.

«Бери и Делай» подсказывает, с помощью каких способов и приемов можно научиться решать задачи с закономерностями.

Какие бывают закономерности в математике

Математическая закономерность — это правило, которое задает порядок элементов в ряду, отражает какое-то изменение этих элементов или их свойств. Математические закономерности бывают:

• Возрастающими, если числовое свойство такой закономерности увеличивается согласно какому-то закону или формуле. К примеру, дерево растет, прибавляя каждый год по 1 новому кольцу на стволе. Зная эту закономерность, мы можем определить точный возраст дерева, посчитав число колец на срезе ствола.
• Убывающими, если числовое свойство такой закономерности уменьшается согласно какому-то закону или формуле. Например, зная, сколько бензина тратит машина, преодолевая каждый километр, мы можем определить, в какой момент нужно будет остановиться и дозаправиться.
• Циклическими, если закономерность имеет свойство повторяться. В таком случае полный круг в циклической закономерности называется циклом закономерности. Смена дня и ночи, времен года, дней недели — это примеры циклических закономерностей.
• Сложными, если они состоят из закономерностей нескольких видов или имеют несколько свойств.

Зачем решать задачи на закономерности

Поиск закономерностей в заданиях помогает детям понять, что из себя представляют числа, и развить способности к наблюдению. Когда ребенок видит закономерность, он изучает ее и может прогнозировать то, что произойдет следом по порядку. Это является важным навыком для понимания чисел и в будущем поможет при изучении более сложных тем математики.

Как решать задачи на закономерности

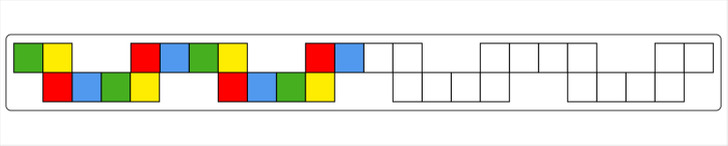
Посмотрите на картинку выше. Это простая задачка, где ребенку предлагают закрасить остальные квадратики, соблюдая заданную закономерность.

Сначала нужно определить цепочку (последовательность цветов), которая повторяется. На картинке выше видно, что цветные квадратики стоят друг за другом в определенном порядке, который не нарушается. Из этого можно сделать вывод, что в данном случае закономерность задана повторением цветов: зеленый, желтый, красный, синий, снова зеленый и так далее. Другими словами, мы имели дело с циклической закономерностью.

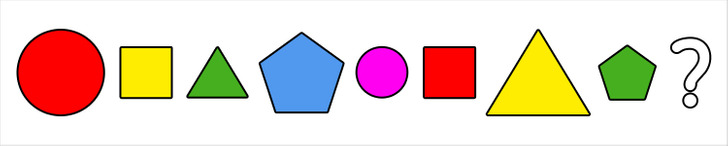
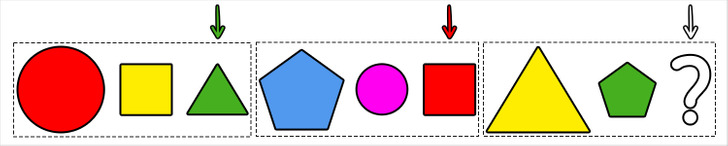
Выше представлена более сложная задачка. Чтобы определить, какая фигура должна быть на месте вопросительного знака, нужно разглядеть несколько закономерностей:

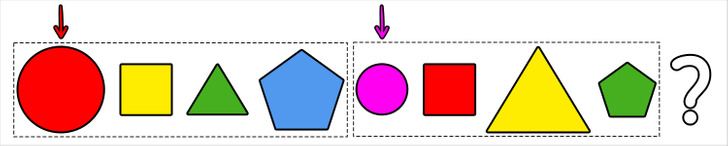
1. Закономерность по форме фигуры заметна, если приглядеться к тому, как чередуются звенья цепочки через каждые 4 элемента. Таким образом, можно сделать вывод, что на месте вопросительного знака должен быть круг.

2. Закономерность по размеру фигуры бросается в глаза, если разделить ряд фигур на части, в каждой из которых всего 3 элемента. Получается, что на месте вопросительного знака должен быть маленький круг.

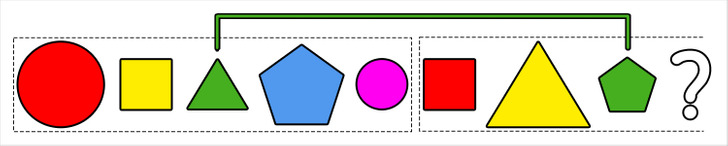
3. Закономерность по цвету становится заметной, если выделить цепочку из 5 элементов. Так мы приходим к выводу, что на месте вопросительного знака находится маленький круг синего цвета. Мы решили задачку, где присутствовала сложная закономерность.

Чтобы решать задачи с закономерностями, удобно сразу выработать алгоритм поиска закономерностей:

• Шаг № 1: Определяем количество свойств цепочки.
• Шаг № 2: Выявляем закономерности для каждого свойства.
• Шаг № 3: Сопоставляем закономерности для определения всех свойств следующего звена в цепочке.

Примеры задач с закономерностями и решения

Задача № 1

Попробуйте отгадать, какая фигура должна быть в последней клетке.

Решение: По горизонтали в ряд после квадрата идет треугольник, после треугольника — круг, а после круга — снова квадрат. По вертикали в ряд после квадрата следует круг, после круга — треугольник, а после него — снова квадрат. Фигуры повторяются по диагонали слева направо. По диагонали справа налево смайлики тоже повторяются в определенном порядке. Получается, что в пустой клетке должен быть квадрат с горизонтальной черточкой вместо улыбки.

Ответ: Квадрат.

Задача № 2

На картинке выше квадраты различаются цветами и числами, записанными внутри них, но располагаются в определенном порядке. Попробуйте определить закономерность.

Решение: В данном случае нужно искать правило, которое задает порядок между числами. Чтобы увидеть закономерность, произведем вычисления:

23 − 14 = 9

14 − 8 = 6

8 − 5 = 3

Получается, что каждое следующее число в цепочке 5, 8, 14, 23 увеличивается на предыдущее значение + 3. Таким образом:

? − 23 = 9 + 3

? = 35

Ответ: Вместо вопросительного знака должно стоять число 35.

Задача № 3

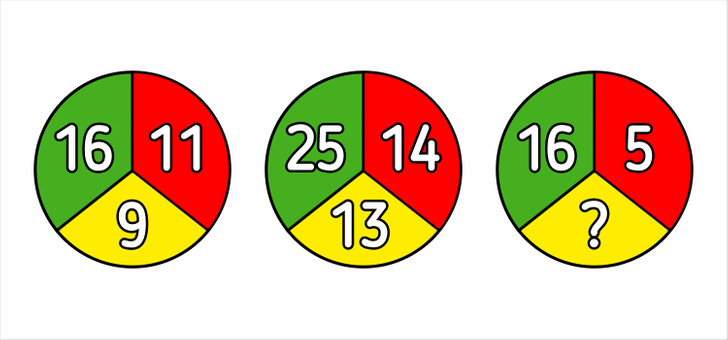
Выше на картинке изображены 3 круга, каждый из которых разделен на 3 сектора. Нужно узнать, какое число кроется за вопросительным знаком.

Решение: В первых 2 кругах число, которое располагается в нижнем секторе, составляет 1/3 от суммы чисел, располагающихся в верхних секторах. Соответственно, чтобы узнать, какое число прячется за вопросительным знаком, нужно сложить числа в 2 верхних секторах 3-го круга и разделить полученное число на 3.

16 + 5 = 21

21 : 3 = 7

Ответ: 7.

Задача № 4

Выше изображена последовательность чисел. Ее надо изучить и найти лишнее число, которое не обладает свойством, характерным для остальных чисел в ряду.

Решение: Все числа в этом ряду делятся на 9, кроме числа 426.

Ответ: 426.

Задача № 5

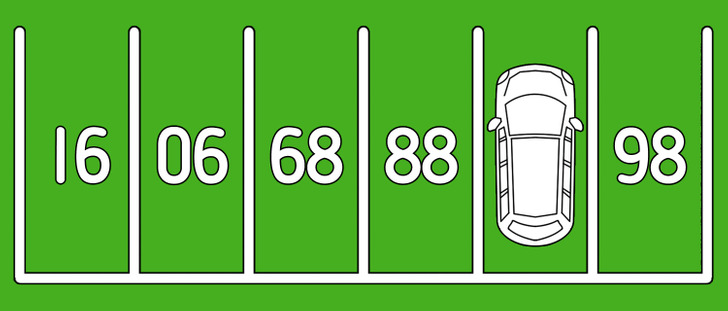
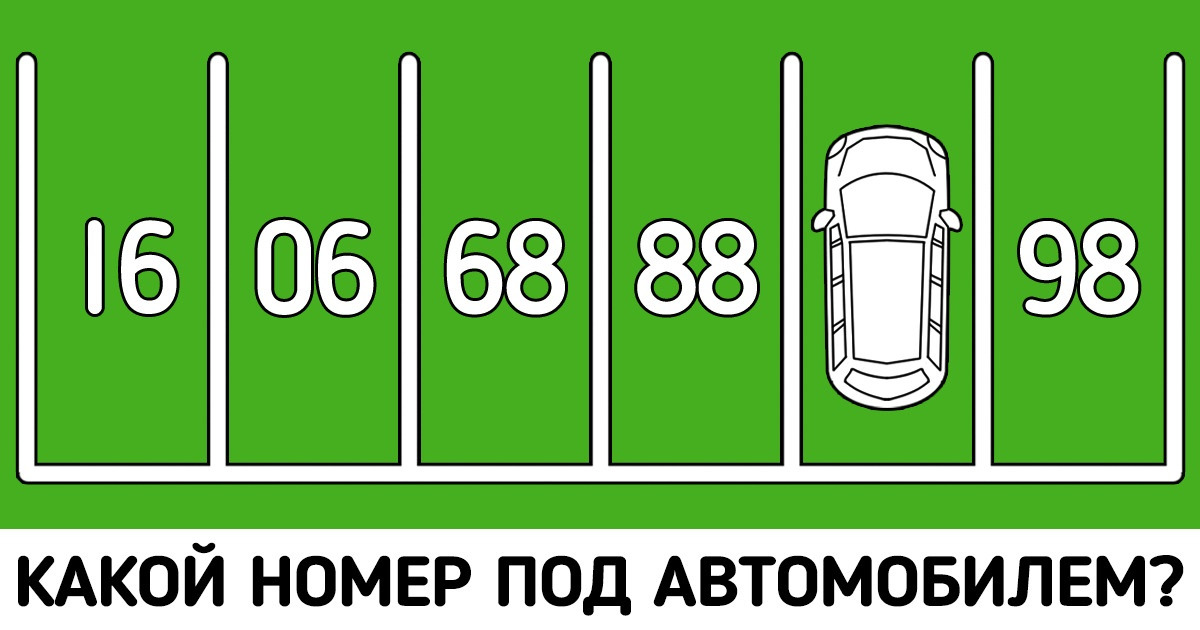
Посмотрите на картинку выше и определите, какое число скрывается под автомобилем.

Решение: Это загадка с подвохом. Достаточно перевернуть картинку вверх ногами, чтобы увидеть последовательность, где каждое последующее число больше предыдущего на 1. Получается, что у нас есть ряд чисел (86, ?, 88, 89, 90, 91), и машина стоит на числе 87.

Ответ: 87.