Как объяснить ребенку, что такое дроби

Школьникам достаточно непросто освоить тему дробей и операций над ними. Но если заранее познакомиться с основами через игру и знакомые понятия, можно избежать трудностей в учебе.
«Бери и Делай» предлагает простое руководство, благодаря которому даже ребенок дошкольного возраста легко разберется в том, что такое дроби.
Что такое дробь
У нас есть одна вкусная пицца и два голодных человека. Разделим целую пиццу на две равные части, чтобы каждый получил половину. Половина, или 1/2 пиццы, — это и есть дробь. Две половины дают целое.
Из примера выше можно сделать два вывода:
- дробь это часть от целого
- дробь меньше целого числа
Допустим, у нас была пицца, и мы поделили ее на четыре части. Один такой кусок уже съели. В итоге у нас осталось три куска из четырех. Это количество можно записать в виде числа 3/4. На бумаге разделяющая черта может быть записана как горизонтальная или косая.
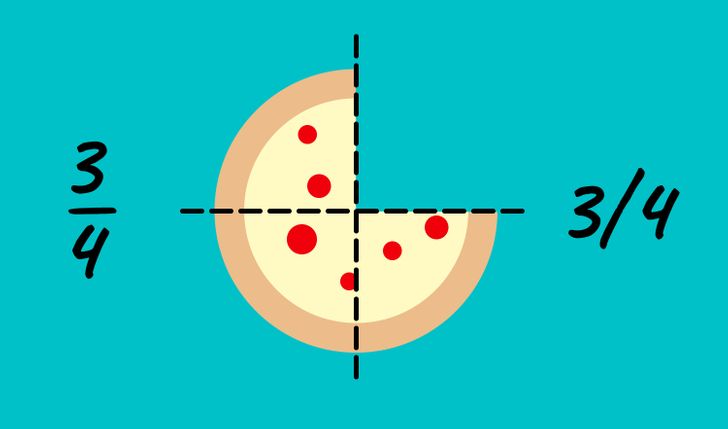
- Нижнее число (или правое) — это знаменатель: оно говорит нам, на сколько частей разделили целое число.
- Верхнее число (или левое) — это числитель: оно сообщает нам, с каким количеством этих частей мы имеем дело.
Когда мы разделяем целое число на части, то чем больше этих частей, тем они меньше, и наоборот. Например, у нас две пиццы: одну мы поровну разделили между двумя людьми, а другую — между четырьмя. В первом случае каждый человек получил половину пиццы (1/2), а во втором — только четверть (1/4).
Благодаря подобным простым примерам и подручным средствам можно объяснить детям, как делить целое на части и какие простые действия можно совершать с дробями.
Способ № 1: Используем детский конструктор

Чтобы показать разные части одного целого, хорошо подходят детали из конструктора Lego. Количество шипов на каждом кирпичике помогает лучше передать суть понятия частей от целого.
- Если за целое мы принимаем деталь с восемью шипами, то квадратная деталь с четырьмя шипами будет половиной, с шестью — 3/4, а деталь с одним шипом — это 1/8.
- Когда в качестве целого выступает длинная деталь, на которой четыре шипа, то 1/2 будет деталь с двумя шипами, а 1/4 — деталь с одним шипом.
- Если в качестве целого у нас выступает длинная деталь, на которой три шипа, то 2/3 будет символизировать деталь с двумя шипами, а 1/3 — деталь с одним шипом.
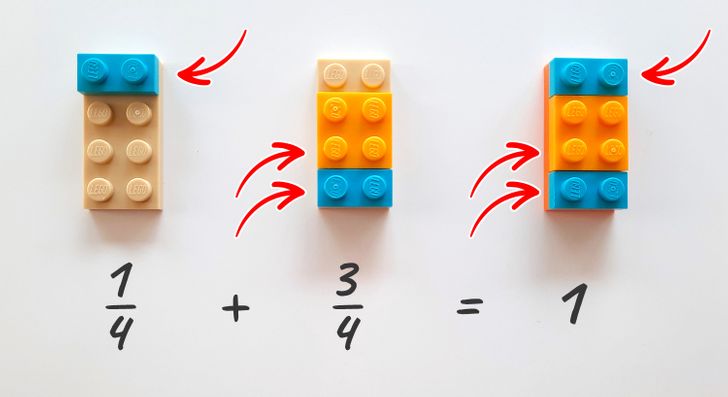
Далее похожим образом можно объяснить простые действия с дробями, у которых одинаковый или общий знаменатель. На картинке выше таким образом мы складываем 1/4 и 3/4, получая в результате целое. Использование в данном случае деталей разного цвета помогает увидеть, какое место в целом займет каждая его часть в результате сложения.
Задание: используя детали Lego как в примере выше, попробуйте вместе с ребенком складывать и вычитать дроби с общим знаменателем.
Способ № 2: Разделяем круги на доли
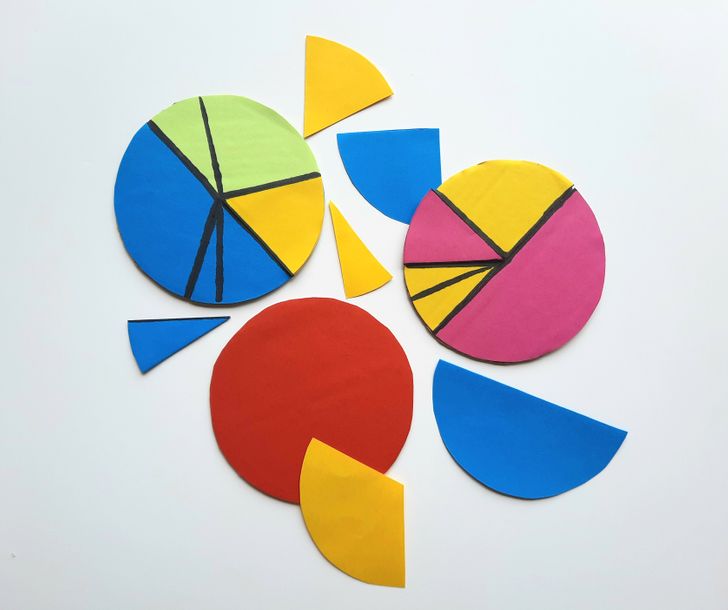
Дробь можно представлять в виде доли от целого. Понимание, как выглядят те или иные доли, помогут ребенку не только делиться пиццей или другими круглыми лакомствами с друзьями, но и различать время на обычном циферблате: так легче будет объяснить, что такое четверть часа и сколько времени пройдет, когда стрелка часов пройдет половину круга.
Чтобы объяснить деление на доли, из картона вырезаете три одинаковых круга.
- Первый круг полностью заклеиваете цветной бумагой одного цвета. Он будет символизировать целое.

- Второй круг разделяете на две половины, прочертив линию обычным карандашом. Заклеиваете одну половину цветной бумагой. Вторую половину тоже заклеиваете бумагой контрастного цвета, после чего снова делите пополам, чтобы получить две четверти. Одну из четвертей снова делите пополам, получив две восьмые доли. Одну из этих восьмых долей заклеиваете цветной бумагой. В результате вы получили круг, разделенный на одну половину, одну четверть и две восьмых.
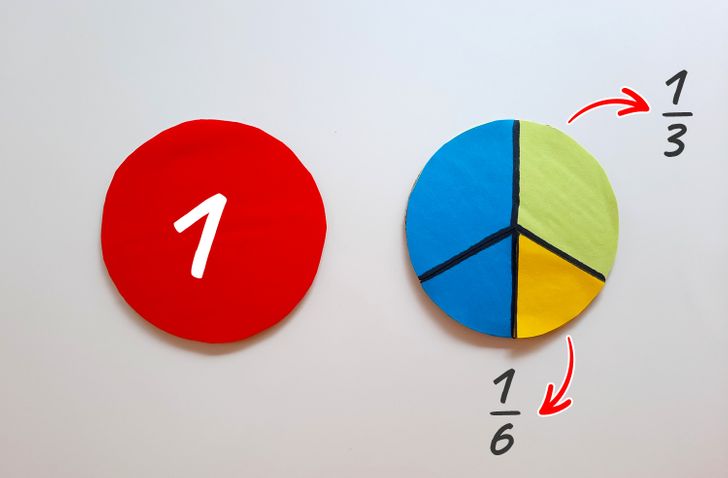
- Теперь третий круг разделяете на три равные части. Одну треть заклеиваете цветной бумагой. Другую треть делите пополам, чтобы получить две доли, равные 1/6 круга. Одну из них заклеиваете бумагой контрастного цвета. У вас остается половина круга, которую вы также заклеиваете цветной бумагой. Так вы сможете продемонстрировать, какую часть от целого занимает 1/3 и 1/6, а также что при сложении они образуют 1/2 целого круга.

В дополнение можно вырезать из цветной бумаги отдельные доли, чтобы накладывать их на целое (самый первый круг) и таким образом наглядно отображать их значение, а также проводить простые операции по сложению и вычитанию внутри круга.
Задание: попробуйте вместе с ребенком собрать целый круг, используя разные комбинации его долей.
Способ № 3: Заполняем шкалу по частям

Целое число можно представлять в виде шкалы, где дроби это деления шкалы. Нарисуйте на большом листе с помощью маркера и линейки шкалу, состоящую из 12 делений. Они могут выглядеть так, как на картинке выше. Каждое деление равняется 2 см в длину. Теперь возьмите пластилин и скатайте из него маленькие шарики размером с вишню.

Предложите ребенку взять один шарик и положить его так, чтобы он занял одно деление. Чтобы заполнить всю шкалу, нам нужно 12 таких шариков, но у нас только один. Таким образом, у нас есть 1/12 от целого.

Теперь добавим еще один шарик на шкалу. Его можно положить к первому и даже склеить с ним, чтобы получилась пара. Если взять шесть таких пар, мы заполним всю шкалу. Но у нас только одна из шести, или 1/6 от целого. Из этого можно сделать еще один вывод:
- 1/6 = 1/12 +1/12

Теперь добавим еще один шарик. Чтобы заполнить всю шкалу, нам нужно всего четыре таких тройки шариков. Пока у нас лишь четверть, или 1/4, от всего необходимого количества, чтобы заполнить шкалу. Из этой картинки следует, что:
- 1/4 = 1/12 +1/12 +1/12
- 1/4 = 1/6 +1/12
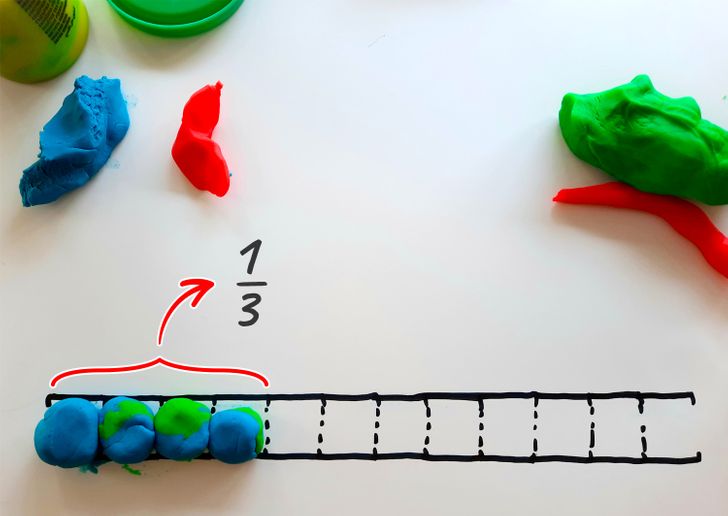
Добавим еще один шарик, чтобы заполнить сразу четыре деления. Для всей шкалы нам нужно три таких группы. У нас в наличии только одна из трех, или 1/3. Если вспомнить, что одно деление у нас означает 1/12, а два деления — это 1/6, то получается, что:
- 1/3 = 1/12 +1/12 +1/12 +1/12
- 1/3 = 1/6 + 1/6
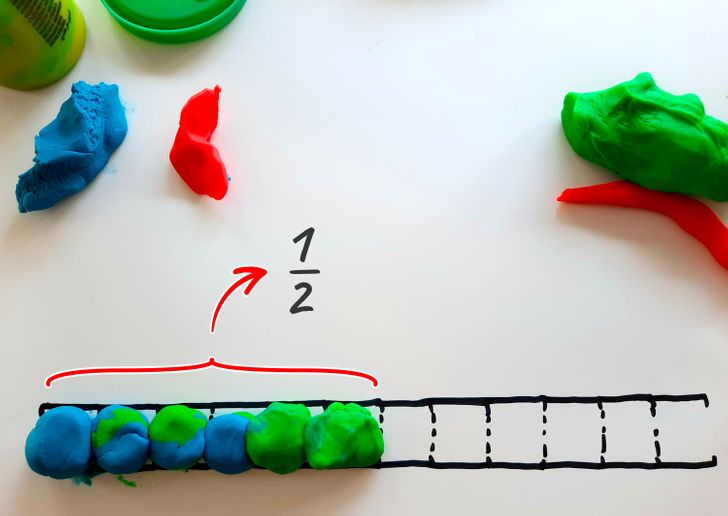
Теперь добавим два шарика на шкалу, чтобы в итоге получилось шесть. Так мы заполнили половину делений, или 1/2. Из этого можно сделать вывод, что:
- 1/2 = 1/12 +1/12 +1/12 +1/12 +1/12 +1/12
- 1/2 = 1/6 + 1/6 + 1/6
- 1/2 = 1/3 +1/6
- 1/2 = 1/4 +1/4
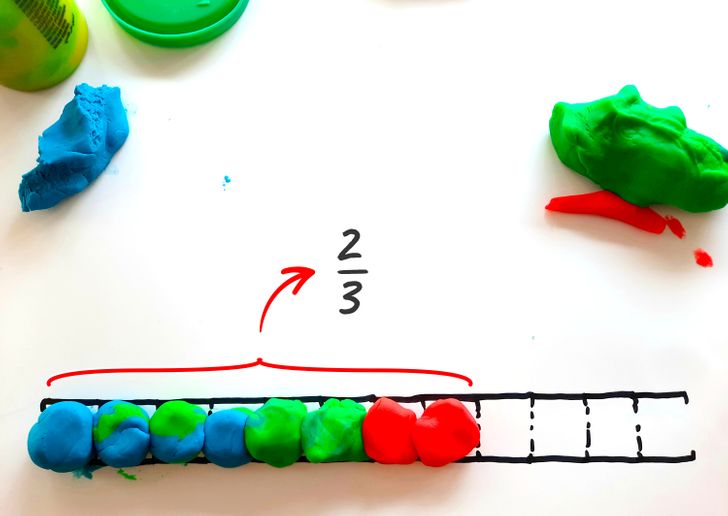
Прибавим еще пару шариков, чтобы получилось восемь. Так мы заполнили 2/3 от целой шкалы. Из чего состоят две трети?
- 2/3 = 1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12
- 2/3 = 1/6 + 1/6 + 1/6 + 1/6
- 2/3 = 1/3 +1/3
- 2/3 = 1/4 + 1/4 + 1/6
- 2/3 = 1/2 + 1/6

Заполним шариком еще одно деление. Так у нас закроется девять клеточек. Это три четверти от всей шкалы. Каким образом можно представить это число?
- 3/4 = 1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12 +1/12
- 3/4 = 1/6 + 1/6 + 1/6 + 1/6 +1/12
- 3/4 = 1/3 +1/3 +1/12
- 3/4 = 1/2 + 1/6 +1/12

И наконец, если добавить еще три шарика, мы заполним всю шкалу, получив целое число.
Способ № 4: Обозначаем соотношение

Нарисуйте семь человечков. Пусть они различаются по цвету одежды и волосам, по позам и наличию тех или иных предметов. В данном случае в качестве целого мы рассматриваем группу человечков.

У двух из семи (2/7) в руках есть воздушный шарик, а у пяти из семи (5/7) его нет. В данном случае дробь не просто делит целое, а помогает обозначить соотношение.
Таким образом делить можно все. В качестве альтернативного примера можно рассмотреть кружку горячего шоколада:
☕ = 🍫🍫 / 🥛🥛🥛
которая на 2/5 состоит из вкусного шоколада и на 3/5 из свежего молока.
Что такое десятичные дроби

Возьмите лист бумаги и нарисуйте на нем квадратную таблицу из 100 клеток. Мы будем принимать ее как целое, разделенное на 100 одинаковых частей-клеток.
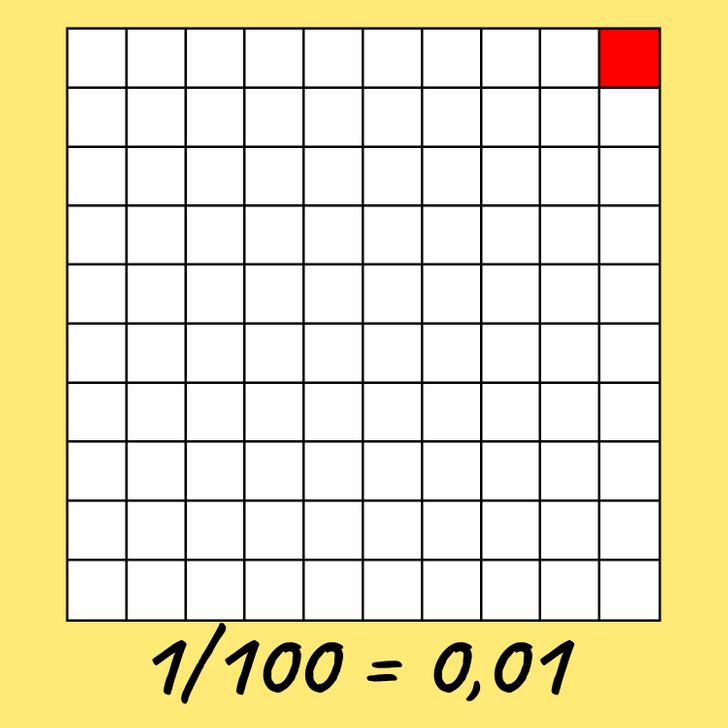
Теперь закрасим одну клетку. Это одна из 100 частей таблицы. Такое число в виде обыкновенной дроби выглядит как 1/100. Но его можно записать в строчку через запятую, чтобы отделить целую часть от дробной:
1/100 = 0,01
Все, что стоит слева от запятой, это целое число. Все, что стоит справа, это части целого числа — десятые, сотые, тысячные, десятитысячные и более мелкие, но всегда кратные десяти. Другими словами, если знаменатель простой дроби равен 10, 100, 1 000, 10 000 и тому подобным числам, то речь идет о десятичной дроби. Такая запись упрощает вид дроби, например:
- 0,8 это 8/10,
- 14,89 это 1 489/100,
- 3,14 159 это 314 159/100 000.
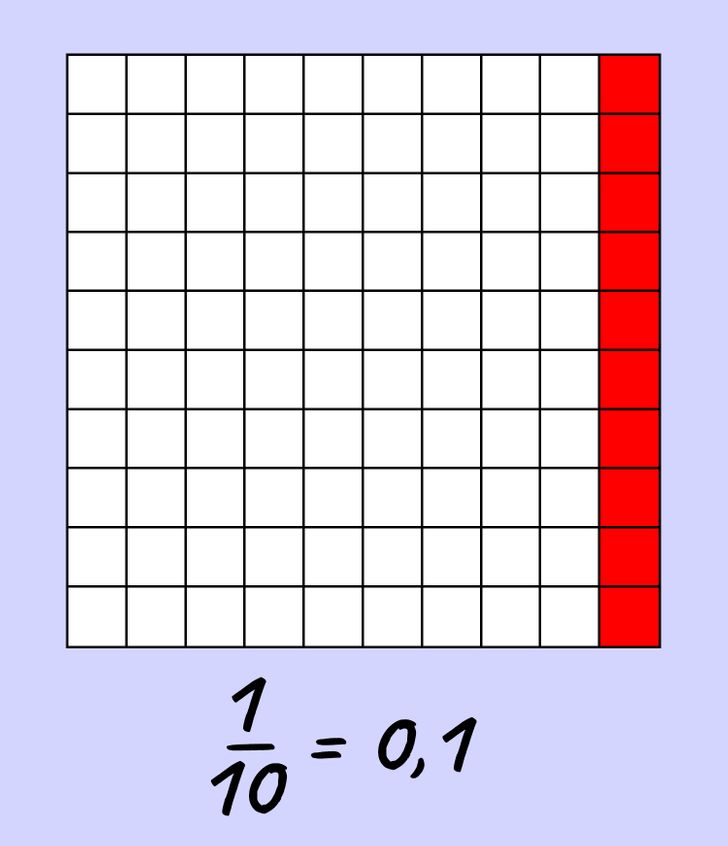
Теперь давайте закрасим в таблице всю колонку. Из 10 таких колонок состоит вся таблица, поэтому можно сказать, что одна колонка равняется одной десятой части таблицы.
Вместо 1/10 такое число запишем как 0,1.
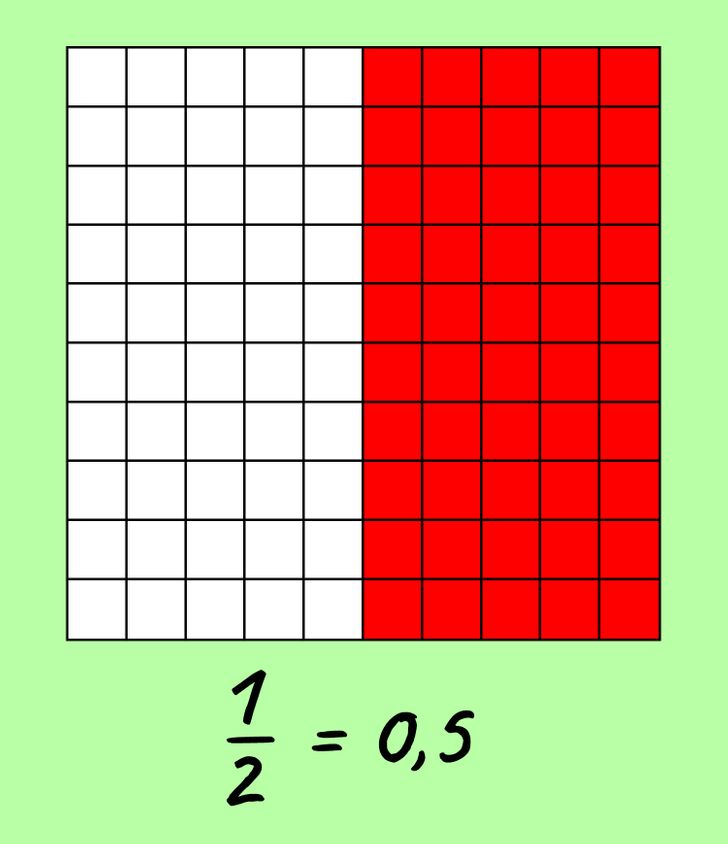
Если закрасить еще четыре колонки, то можно будет сказать, что мы закрасили пять десятых, или 0,5. На картинке выше видно, что это ровно половина, или 1/2 таблицы.
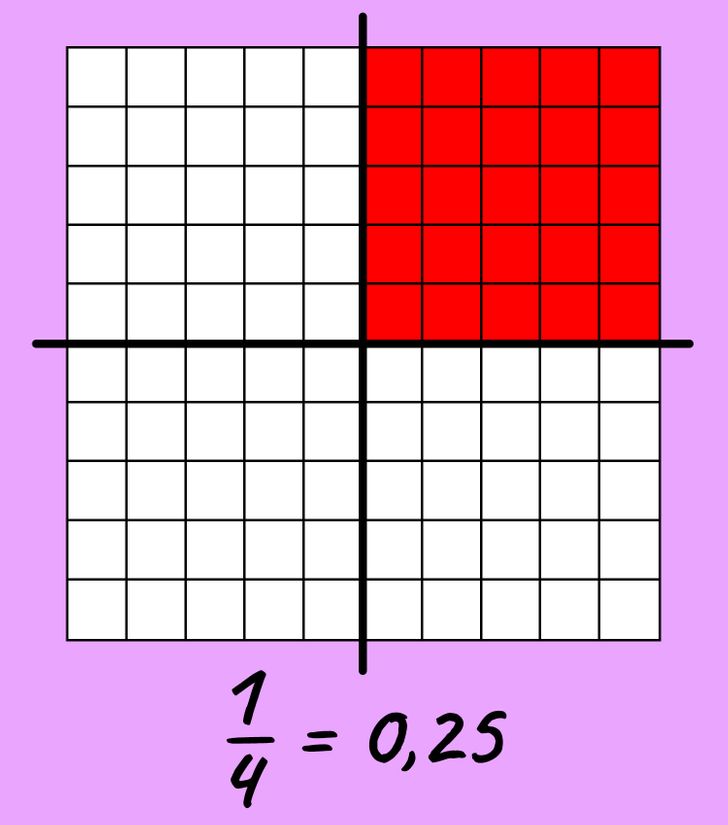
Допустим, что мы снова взяли пустую таблицу и разделили ее линиями на четыре равные части. Одну часть закрасили: в ней оказалось 25 клеток из 100, или 0,25. Таким образом, мы видим, что 1/4 = 0,25.
Получается, что одни и те же числа можно записывать в виде обыкновенных и десятичных дробей:
- 3/4 = 0,75
- 1/2 = 0,5
- 1/4 = 0,25
- 1/5 = 0,2
- 1/10 = 0,1
- 1/100 = 0,01
Задание: нарисуйте несколько пустых квадратных таблиц из 100 клеток и предложите ребенку закрасить клетки, представляя разные десятичные дроби и обыкновенные дроби, сравнивая их между собой. Это поможет ему визуально увидеть и запомнить, что, например, 3/4 это больше, чем 0,3 или 0,4.