Какие бывают математические символы и когда их использовать
Символы помогают сократить и упростить текст математических выражений. Они используются для обозначения арифметических действий, сравнения математических объектов, задания условий выражения или структурирования других символов в формуле.
«Бери и Делай» рассказывает, какие бывают математические символы и как правильно их использовать.

🟡 Плюс ( + ) используется для операций сложения (например, 2 + 2).
🟡 Минус ( − ) используется для операций вычитания (например, 4 − 2) или обозначения отрицательных чисел (например, −2).
🟡 Знак умножения ( × ) используется для операций умножения (например, 2 × 2). Вместо него также может использоваться точка ( · ) или звездочка ( * ).
🟡 Знак деления ( : ) используется для операций деления (например, 4 : 2) или обозначения соотношения двух величин (например, 1:1). Для операций деления также может использоваться косая черта ( / ).

🟠 Знак равенства ( = ) используется для обозначения равенства (например, (5 × 6) = (3 × 10)) или результатов математических действий (например, 5 + 6 = 11).
🟠 Знак неравенства ( ≠ ) используется для обозначения неравных между собой по значению математических объектов или частей выражения (например, 2 ≠ 3).
🟠 Знак приблизительного равенства ( ≈ ) используется для обозначения приблизительных значений и читается как «приблизительно равно» (например, число π ≈ 3,14).
🟠 Знак тождественности ( ≡ ) используется для обозначения равенства, которое истинно, какие бы значения ни имели его переменные. Например, части выражения а + (−а) ≡ 0 будут тождественны вне зависимости от того, какое значение будет иметь переменная а.

🟣 Знак «меньше» ( < ) используется для обозначения строгого неравенства, где одно число меньше другого (например, 2 < 3).
🟣 Знак «больше» ( > ) используется для обозначения строгого неравенства, где одно число больше другого (например, 3 > 2).
🟣 Знак «меньше или равно» ( ≤ ) используется для обозначения неравенства, где одна часть меньше или равна другой (например, выражение а ≤ b означает, что а < b или a = b).
🟣 Знак «больше или равно» ( ≥ ) используется для обозначения неравенства, где одна часть больше или равна другой (например, выражение а ≥ b означает, что а > b или a = b).

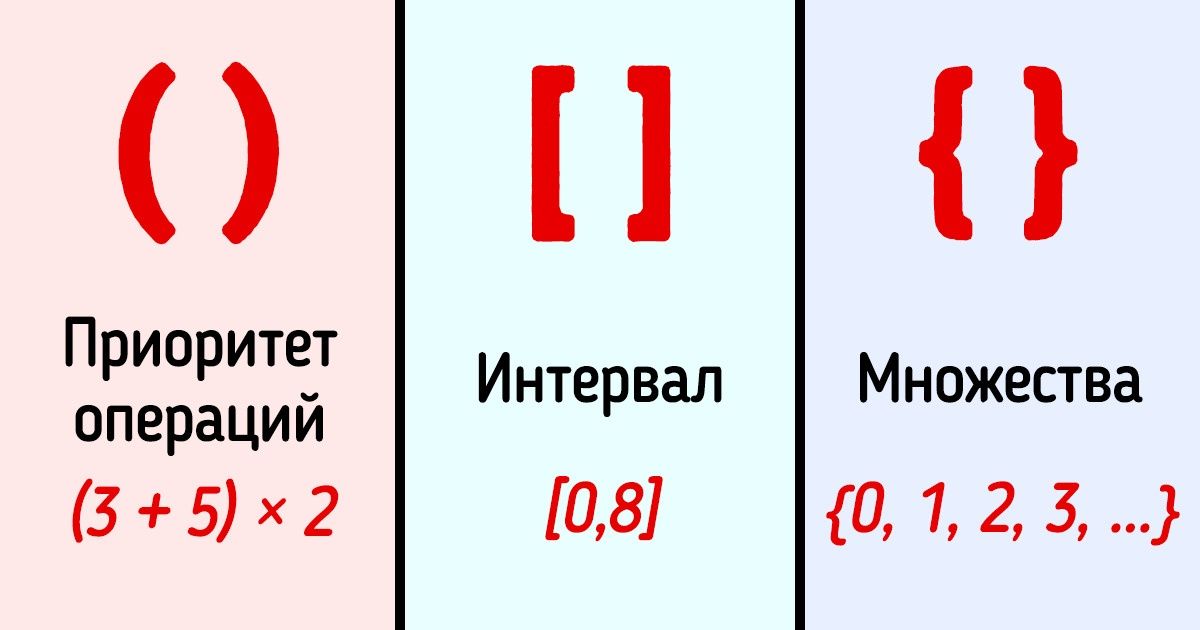
🟢 Круглые скобки ( ) используются для обозначения приоритета математических операций. Например, выражение (3 + 5) × 2 означает, что сначала надо сложить 3 и 5, а потом умножить их сумму на 2. Также круглые скобки используются для выделения аргументов функции (например, f ( x ) — это функция f, примененная к переменной x).
🟢 Квадратные скобки [ ] используются для обозначения приоритета операций в качестве скобок второго уровня. Например, выражение [(3 + 5) × 2]² означает, что сначала надо сложить 3 и 5, потом умножить их сумму на 2, а конечный результат операции возвести во вторую степень. Также квадратные скобки могут обозначать интервалы. Например, [0,8] представляет собой набор чисел от 0 до 8 включительно.
🟢 Фигурные скобки { } используются для обозначения множеств. Например, множества натуральных чисел — {0, 1, 2, 3, ...}.
Прочие математические символы

🔵 Знак плюс-минус ( ± ) используется для написания диапазона значений. Например, 15 ± 3 означает, что значение лежит в диапазоне от 12 до 18.
🔵 Знак квадратного корня ( √ ) обозначает квадратный корень из определенного числа. Например, √4 читается как «квадратный корень из четырех», а результат операции равен 2.
🔵 Знак бесконечности ( ∞ ) означает, что результат вычисления не ограничен. Может употребляться со знаками плюса или минуса.