Какие части окружности бывают и чем они различаются

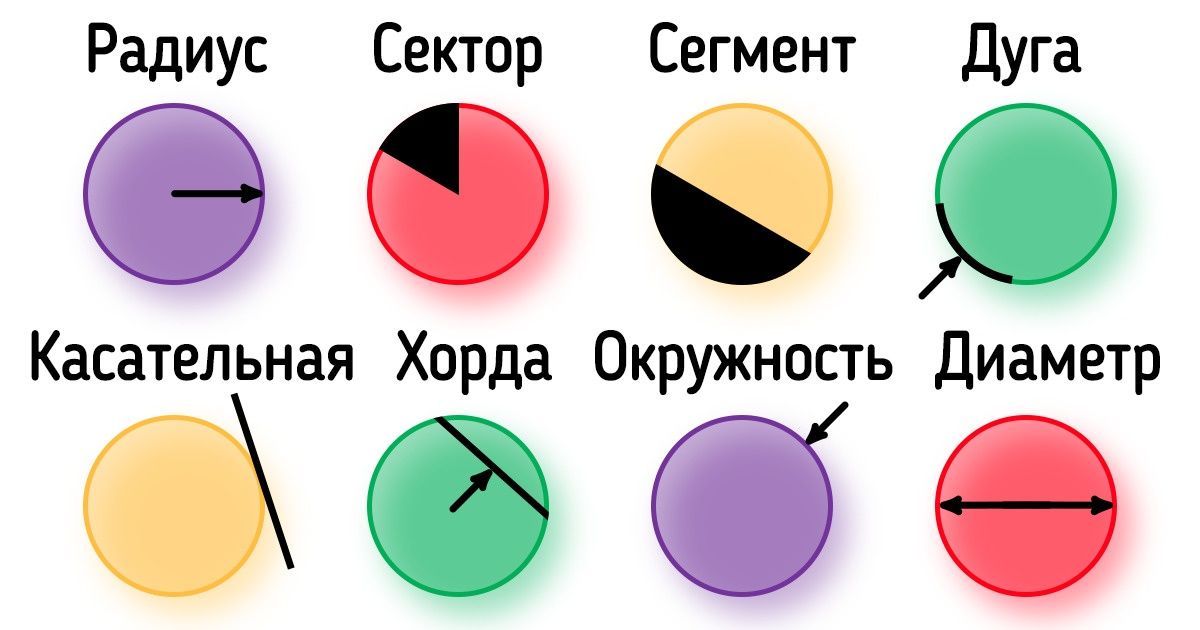
В реальной жизни мы достаточно часто имеем дело с окружностью и ее элементами, хотя не всегда замечаем это. К примеру, зная диаметр колеса, как можно узнать расстояние, которое оно преодолевает за 1 оборот? Или как узнать, сколько места в саду займет пруд в форме круга, если вам известен его радиус?

«Бери и Делай» помогает разобраться, что представляет собой окружность, чем отличны и примечательны ее элементы.

Что такое окружность

Если взять множество точек и расположить их последовательно друг за другом, у вас получится линия. Если она не искривляется, не имеет ни начала, ни конца и бесконечно продолжается в обе стороны, то это прямая. Если линия изгибается из-за определенного расположения точек, то это кривая. Концы кривой линии, в свою очередь, могут не соединяться, образуя незамкнутую линию. Когда же они соединяются, получается замкнутая линия.

Нарисуйте замкнутую кривую линию так, чтобы все ее точки находились в одной плоскости и на равном расстоянии от заданной точки, которая располагается в той же плоскости, и вы получите отдельную геометрическую фигуру под названием окружность. Если взять только плоскость внутри окружности, то вы получите другую геометрическую фигуру под названием круг.

Чтобы построить окружность, используется циркуль — специальный инструмент, позволяющий чертить окружности и дуги.

Что представляют собой элементы окружности

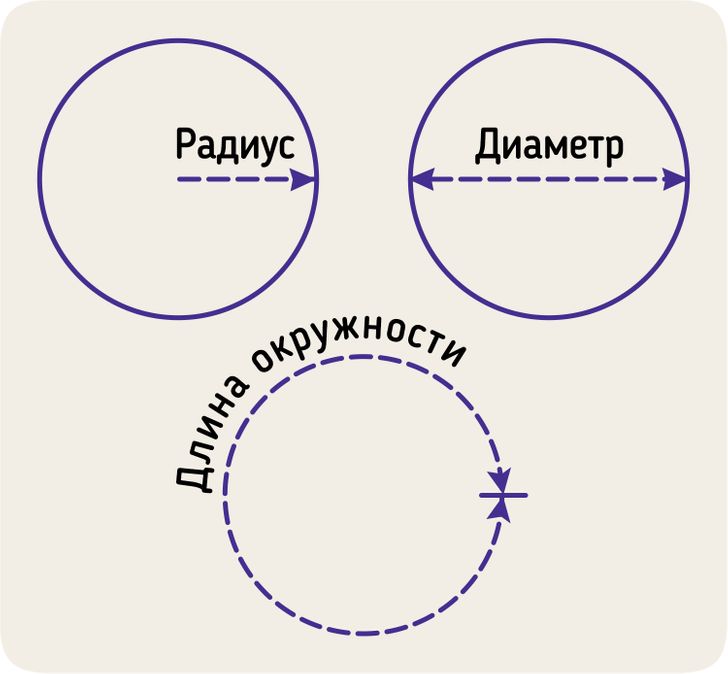
• Длина отрезка от центра окружности до любой ее граничной точки всегда едина и называется радиусом.
• Отрезок, который соединяет 2 любые точки окружности и проходит через центр окружности, называется диаметром. При этом диаметр окружности всегда в 2 раза больше ее радиуса.
• Если измерить длину замкнутой плоской кривой, ограничивающей круг, получится длина окружности. Также можно сказать, что длина окружности является частным случаем периметра, если рассматривать окружность как границу круга.

Обозначим радиус буквой R, диаметр — буквой D, а длину окружности — буквой L. В определении диаметра выше говорится, что диаметр окружности всегда в 2 раза больше ее радиуса:

D = 2R

Если взять длину окружности и разделить ее на диаметр окружности, вы всегда получите одно и то же число — число пи (π). Оно неизменно, иррационально и имеет бесконечное количество цифр после запятой:

π ≈ 3,1415926535897932384626433832795...

Таким образом, чтобы узнать длину окружности, достаточно умножить число π на ее диаметр или на 2 радиуса:

L = π × D = π × 2R

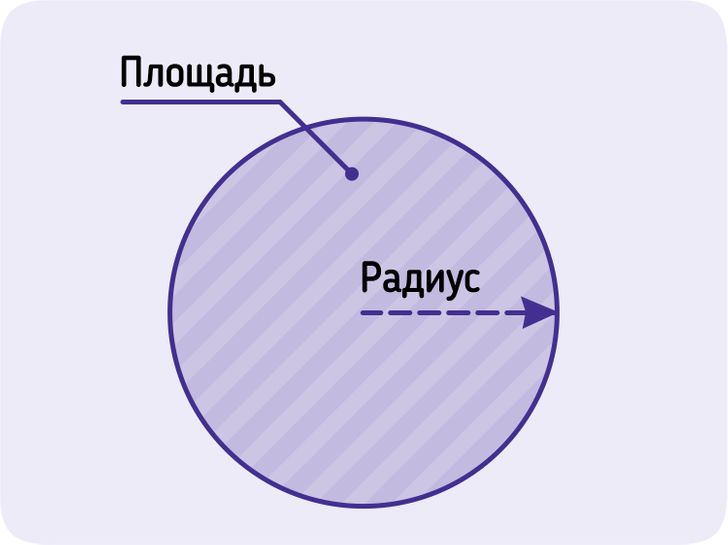
Зная радиус, легко вычислить площадь круга. Для этого нужно число π умножить на квадрат радиуса круга:

S = π × R² = (π × D²) : 4

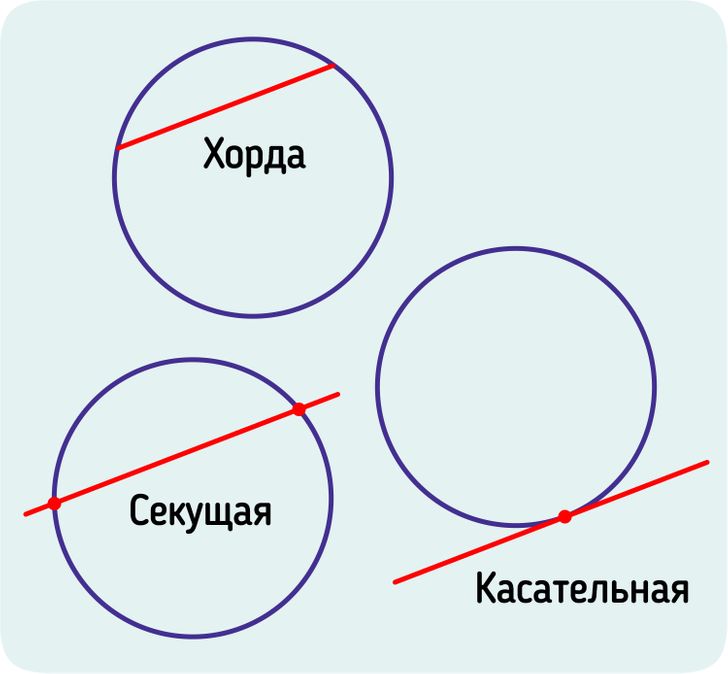
• Отрезок, соединяющий 2 любые точки окружности, называется хордой.
• Прямая, которая соединяет 2 любые точки окружности, называется секущей. Таким образом, хорда всегда находится на секущей.
• Если у прямой с окружностью только 1 общая точка, то эта прямая называется касательной. Полезно знать, что касательная всегда перпендикулярна радиусу окружности, проведенному через точку касания. И наоборот: если прямая проходит через точку, расположенную на конце радиуса, лежащего на окружности, и перпендикулярна ему, то она называется касательной.

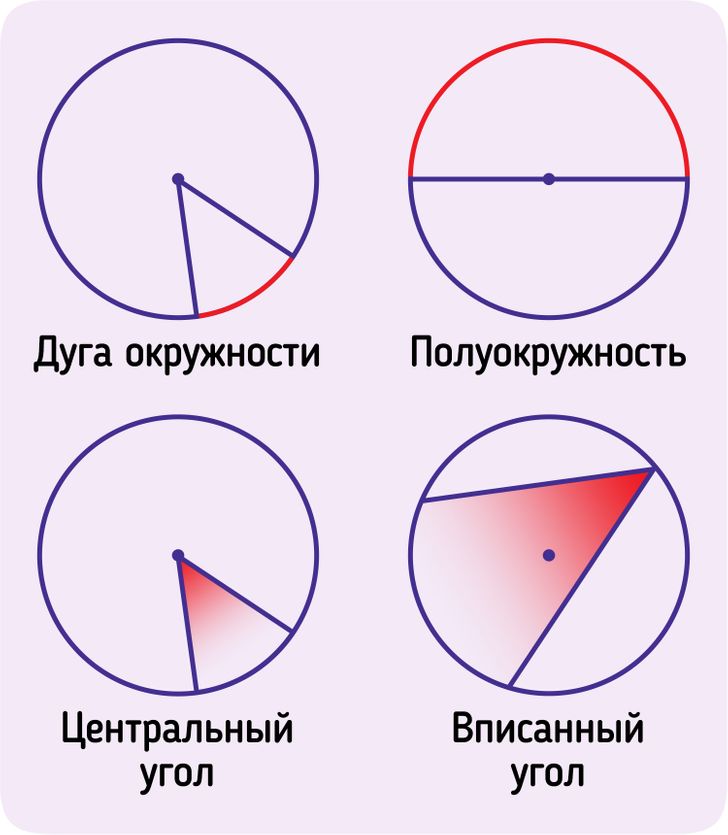
• Часть окружности называют дугой. Она получается благодаря тому, что окружность любые 2 различные и принадлежащие ей точки разбивают на части, каждая из которых называется дугой.
• Дуга, в свою очередь, может быть полуокружностью, если отрезок, который соединяет ее концы, является диаметром окружности.
• Если от каждого конца дуги окружности провести отрезки к центру окружности, то вы получите угол с вершиной в центре окружности, который называется центральным углом. Таким образом, градусная мера дуги равна градусной мере центрального угла, что видно из картинки выше.
• Если вершина угла находится на окружности, а стороны пересекают окружность, то такой угол называется вписанным углом.

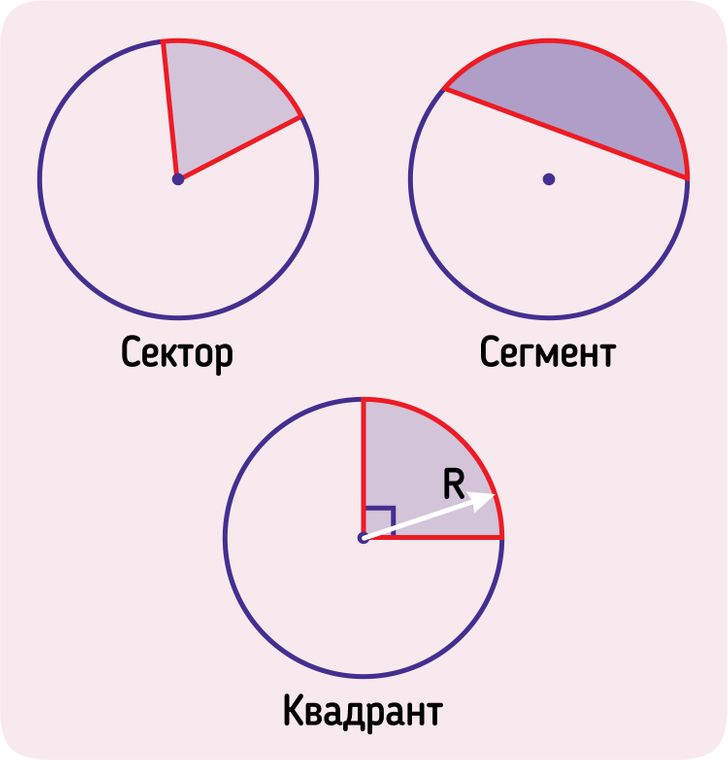
• Часть круга, которая лежит внутри конкретного центрального угла, называется круговым сектором.
• Часть круга, которая заключена между дугой окружности и ее хордой, называется круговым сегментом. Если из середины хорды до пересечения с дугой провести перпендикуляр, вы получите стрелку дуги, которая еще называется высотой сегмента.
• Если сектор отсечен радиусами, образующими угол в 90°, то он называется квадрантом.