Что такое порядок действий и почему люди без него все время путаются

С порядком действий в математике каждый из нас знакомится в школе. Постепенно мы забываем эти правила, из-за чего легко допускаем ошибки в расчетах, которые совершаем в повседневной жизни.

«Бери и Делай» объясняет, чему учит порядок действий в математике, из-за которого даже взрослые часто допускают ошибки в «детских» задачках, и почему его важно знать в любом возрасте.

Зачем соблюдать правильный порядок действий

Основные арифметические операции в математике — это:

• сложение (+)
• вычитание (-)
• умножение (×)
• деление (÷)

Если в числовом выражении используется одна операция, то решить такой пример не составит труда. Например, 3 + 2 = 5 или 6 ÷ 3 = 2. Когда операций 2 или более, то, чтобы получить верный ответ, необходимо выполнять действия в определенном порядке.

Выше изображены 3 примера, каждый из которых легко решить неправильно, если забыть о правильном порядке действий в математике. Попробуйте решить эти примеры самостоятельно, а затем сверьте полученные результаты с правильными ответами в конце статьи. Если хотя бы в одном из них вы ошиблись, возможно, вам стоит повторить вместе с нами правила, касающиеся порядка действий.

Правило № 1. Действия выполняются слева направо по очереди

✅ Выполняя основные арифметические операции над числами, принято двигаться слева направо.

Обратите внимание на картинку выше. Чтобы вычислить результат выражения 6 ÷ 3 × 2, необходимо выполнить действия поочередно слева направо, сначала разделив число 6 на 3, а затем умножив результат на 2. Выполнив операции в ином порядке (сначала умножение, а потом деление), мы получим неверный ответ.

❗ Если выражение состоит только из операций умножения или операций сложения, то, согласно переместительному закону, результат выражения не зависит от того, в какой последовательности выполнены операции.

Правило № 2. Сначала выполняются умножение и деление, затем сложение и вычитание

Одно выражение может содержать несколько разных арифметических операций, как на картинке выше. Запишем это выражение как 2 + 2 × 2. Если выполнить все действия по очереди слева направо, то получим 2 + 2 × 2 = 4 × 2 = 8. Этот ответ неверный (в этом можно удостовериться, пересчитав единичные квадратики на фотографии). Почему так получилось?

✅ Выше мы говорили о 4 основных арифметических операциях. Они неравнозначны по приоритету, что влияет на порядок, в котором нужно решать пример. Умножение и деление имеют больший приоритет, чем сложение и вычитание. Если действие имеет больший приоритет, то оно выполняется в первую очередь.

Применим это на практике и решим пример еще раз: 2 + 2 × 2 = 2 + 4 = 6. Ответ верный.

❗ Если в выражении есть 2 и более равнозначные операции, то их выполняют по порядку слева направо. Таким образом, умножение и деление — это равнозначные операции и порядок их выполнения зависит только от порядка появления в выражении. То же самое касается сложения и вычитания.

Выше показан пример решения выражения 12 ÷ 3 × 6 — 12 ÷ 6 × 3. По правилам, сначала необходимо выполнить деление и умножение, двигаясь слева направо, затем снова деление и умножение в правой части выражения, а только в конце перейти к вычитанию. Если порядок нарушить, ответ будет неверным.

Правило № 3. Возвести число в степень или извлечь корень нужно до перехода к другим операциям

✅ Если в выражении есть число, которое нужно возвести в степень, или произвести обратную операцию (извлечь корень), то это необходимо сделать перед тем, как выполнять основные арифметические операции.

К примеру, попробуем решить, чему равно 4 + 2 +2² + 3². Для этого нужно сначала поочередно возвести в степень тройку и двойку, получив 4 + 2 + 4 + 9, а затем сложить все числа и получить в ответе 19.

❌ Здесь легко допустить ошибку, сложив между собой числа с одинаковыми показателями степени (то есть 2² и 3²), а затем возведя полученную сумму в степень.

Правило № 4. Действия в скобках всегда выполняются в первую очередь

✅ Если часть выражения заключена в скобки, ее нужно решить в первую очередь. Затем вычислить степень или корень числа, после выполнить остальные операции, соблюдая приоритет и двигаясь слева направо.

На картинке выше изображен простой пример. Слева ход решения, где соблюдаются правильный порядок действий: сначала получаем результат в скобках, затем выполняем умножение по очереди слева направо, в конце — операцию сложения. Справа неверный ход решения, где все операции выполняются поочередно слева направо, а в результате получается неправильный ответ.

✅ Между операциями в скобках действуют правила приоритета и очередности решений слева направо.

В длинных выражениях можно проставлять над операциями числа, соответствующие очередности выполнения действий, как в примере выше. Это облегчает процесс решения.

Как запомнить порядок действий

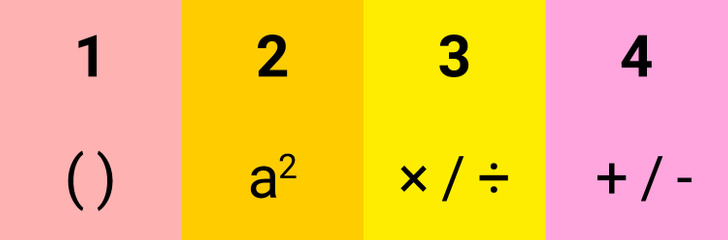
1. Если в выражении есть скобки, сначала выполните действия внутри них.

2. Если в выражении число нужно возвести в степень или извлечь из него корень, сделайте это перед тем, как выполнять другие операции.

3 и 4. Среди 4 элементарных арифметических действий умножение и деление имеют больший приоритет, чем сложение и вычитание, поэтому выполняются в первую очередь. Равнозначные по приоритету операции выполняются по очереди, в порядке слева направо.

Ответы на примеры в начале статьи

• 8 ÷ 4 × 2 = 2 × 2 = 4

Это достаточно простой пример. Вы вряд ли допустили ошибку, так как решали его, инстинктивно выполняя действия по очереди, двигаясь слева направо.

• 6 ÷ 2(1 + 3) = ?

Этот пример выглядит простым, но способен поставить в тупик даже профессоров математики. Это связано с тем, что вы можете получить разные ответы в зависимости от того, как именно решаете его. Например, можно решить так: 6 ÷ 2(1 + 3) = 6 ÷ 2(4) = 3 * 4 = 12. Но если опереться на свойство дистрибутивности (где a(b+c) равняется a × b + a × c), то получается 6 ÷ 2(1 + 3) = 6 ÷ ((2 × 1) + (2 × 3)) = 6 ÷ (2 + 6) = 6 ÷ 8 = ³/₄. Это возникает из-за того, что выражение можно интерпретировать по-разному, в результате чего ответы тоже получаются разными. В каком-то смысле это похоже на ситуации, когда из-за некорректной формулировки и порядка слов в предложении оно приобретает разные смыслы, например, «Как удивили его слова брата!» может означать, как его удивили слова брата, или как его слова удивили брата.

• 3(4 + 1) + 6² ÷ 3 — 7 = 3 × 5 + 6² ÷ 3 — 7 = 3 × 5 + 36 ÷ 3 — 7 = 15 + 36 ÷ 3 — 7 = 15 + 12 — 7 = 20

В этом выражении легко допустить разные ошибки, но правильный алгоритм следующий: сначала выполняется операция в скобках, затем число 6 возводится во 2-ю степень, после нужно выполнить умножение, затем деление, после чего остаются сложение и вычитание. Аналогичный результат получится, если вспомнить свойство дистрибутивности (где a(b+c) равняется a × b + a × c) и решать пример следующим образом: 3(4 + 1) + 6² ÷ 3 — 7 =

((3 × 4) + (3 × 1)) + 6² ÷ 3 — 7 = (12 + 3) + 6² ÷ 3 — 7 = 15 + 36 ÷ 3 — 7 = 15 + 12 — 7 = 20.