Что такое теория вероятностей простыми словами
Представьте, что уличный артист предлагает вам сыграть в игру: он бросает кости, а вам нужно лишь угадать, какое число в сумме выпадет на двух кубиках, чтобы выиграть приз. Предсказать, какое именно число от 2 до 12 выпадет при броске, невозможно. Но если вы загадаете семерку, у вас будет больше шансов выиграть, чем если вы выберете двойку. Именно этому учит нас теория вероятностей.
Мы в «Бери и Делай» простыми словами постараемся объяснить, в чем заключается теория вероятностей.
Что изучает теория вероятностей
Упростим ситуацию с кубиками, взяв обычную монетку. Если подкинуть ее, выпадет одно из двух: орел или решка. Попробуйте подбросить монетку раз 100, и вы увидите, что каждая сторона выпадает примерно одинаковое количество раз. Получается, что с вероятностью 50 % выпадет орел или решка.

Если бросить пару игральных костей, то в сумме выпадет число от 2 до 12 (по количеству очков на сторонах кубиков). Общее количество очков, выпавших на костях, будет значением случайной величины. Другими словами, случайная величина — это численное выражение результата случайного события.
Подбросив вверх монетку, вы получите орла или решку. Это два случайных события. Каждое из них может произойти или не произойти. Событие — это понятие, которое находится в основе теории вероятностей.
Теория вероятностей — это отдельный раздел математики, который изучает закономерности, связанные со случайными явлениями: случайные события, случайные величины, их свойства и операции над ними.
Что такое пространство элементарных событий
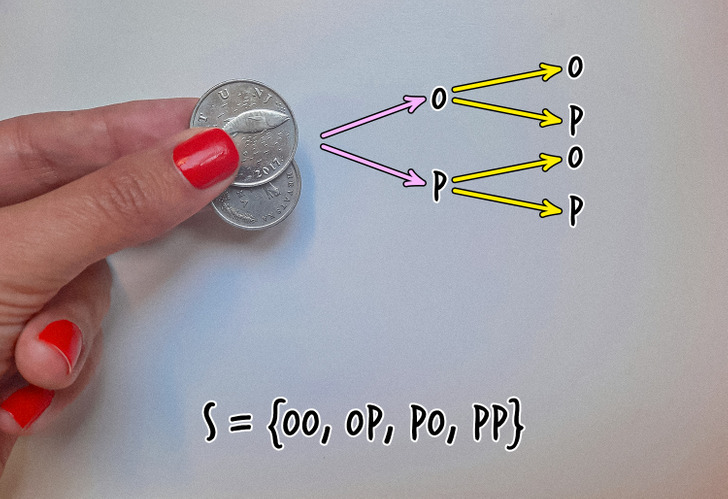
Возьмем две монетки. Если подбросить каждую из них, выпадет орел или решка — одно из двух возможных событий. А сколько возможных событий можно получить, если одновременно подбрасывать сразу две монетки?
Взгляните на картинку выше: на ней буквой Р мы обозначили событие, когда выпадает решка, а буквой О — когда выпадает орел. Допустим, что при первом броске у одной монеты выпал орел, а у второй решка. Тогда при втором броске каждая монетка может упасть вверх снова орлом или решкой, что в итоге даст 4 возможных комбинаций по результатам двух бросков. То, что мы нарисовали выше, называется деревом вероятностей. Оно изображает все возможные независимые события в данном испытании.
Итак, комбинации ОО, ОР, РО и РР представляют собой множество всех различных исходов нашего испытания, называются пространством элементарных событий и обозначаются латинской буквой S.
Как вычислять вероятность с помощью классической формулы
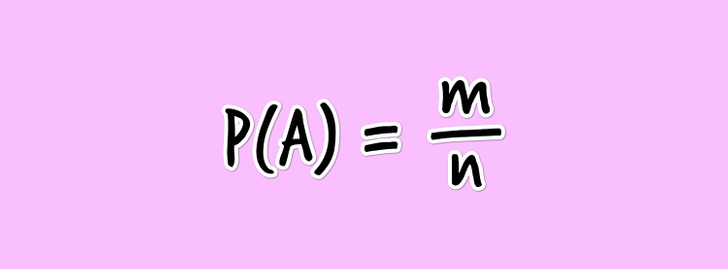
Вероятность того, что событие произойдет или не произойдет в конкретном испытании, можно вычислить, используя формулу:
P (A) = m/n,
где P обозначает вероятность события, A — само событие, о котором идет речь, n — общее число всех различных элементарных исходов этого испытания, m — количество элементарных исходов, благодаря которым событие A может произойти.

К примеру, возьмем упаковку разноцветных конфет. Всего в упаковке 51 конфета, из них 6 конфет синего цвета. Вероятность того, что в этой упаковке вам попадется синяя конфета (событие А в этом случае), равняется: P (A) = m/n. Получается 6/51, или чуть больше 11 % (вместо дроби мы можем записать вероятность в процентах).
- Если в упаковке все конфеты будут синего цвета, то вероятность того, что вы достанете синюю конфету, будет равна: 51/51 = 1.
- Если вы захотите вычислить, какова вероятность того, что вы достанете из этой упаковки фиолетовую конфету, то получите: 0/51 = 0.
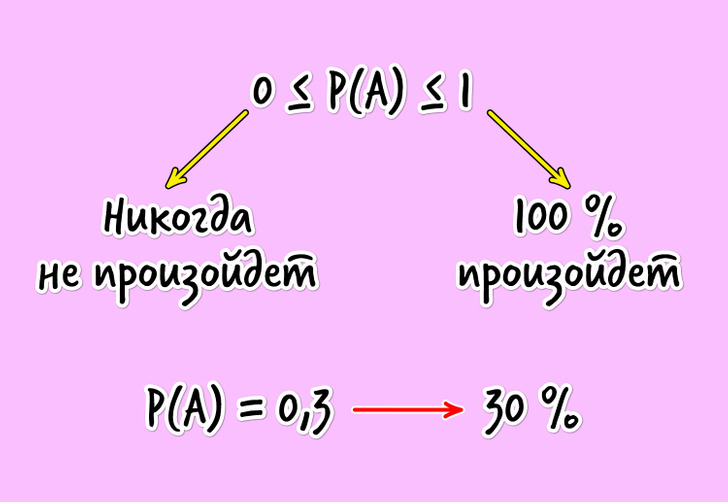
Таким образом, опытным путем мы пришли к пониманию того, что у вероятности есть несколько свойств:
- Если вероятность события равна 1, то оно 100 % произойдет.
- Если вероятность события равна 0, то оно никогда не произойдет.
- Между нулем и единицей будет находиться положительное число, характеризующее вероятность конкретного случайного события. Если вероятность события равняется 0,3, то это означает, что с вероятностью 30 % оно произойдет.
Из этого можно сделать вывод, что для вероятности любого события справедливо 0 ≤ P (A) ≤ 1.
Как решать простые задачи по теории вероятностей
Задача № 1: В корзине лежит 15 разных яблок: 10 зеленых и 5 красных. Какова вероятность достать из корзины желтое яблоко?
Решение: Воспользуемся формулой P (A) = m/n. В данном случае n = 15, а m = 0. Следовательно, вероятность достать из корзины желтое яблоко равняется: P (A) = 0/15 = 0. Другими словами, это невозможно.
Задача № 2: В колоде 36 карт. Из нее вынули одну. Какова вероятность того, что это карта пиковой масти?
Решение: Воспользуемся формулой P (A) = m/n. В данном случае n = 36, а m = 9 (именно столько карт пиковой масти во всей колоде карт). Тогда получается, что вероятность нужного события равна: P (A) = 9/36 = 0,25, или 25 % того, что вы достанете карту пиковой масти.
Теоремы сложения и умножения вероятностей

Представьте, что перед вами 3 кучки, в каждой по 10 деталей конструктора. В первой кучке 8 деталей для строительства домика, во второй — 7, а в третьей — 9, все остальные детальки — для декора и сбора человечков. Вы берете из каждой кучки по одной случайной детали. Какова вероятность того, что все эти три детали подойдут для строительства домика?
Уточним: Если вы берете строительную деталь из одной кучки, это не значит, что вы достанете или не достанете аналогичную из двух других. Другими словами, эти события независимы друг от друга (вероятность наступления любого из них не зависит от остальных событий из рассматриваемого нами множества).
Итак, мы рассматривает три независимых события. Посчитаем вероятность извлечения строительной детали для каждой кучки:
- 1-я кучка: 8/10, или 0,8, или 80 %
- 2-я кучка: 7/10, или 0,7, или 70 %
- 3-я кучка: 9/10, или 0,9, или 90 %
Чтобы узнать вероятность совместного появления этих трех независимых событий, нам нужно перемножить их: 0,8 × 0,7 × 0,9 = 0,504. Получается, что вероятность того, что все три детали окажутся строительными, равняется 0,504, или составляет больше 50 %.

Мы решили эту задачу, воспользовавшись теоремой умножения вероятностей, которая выглядит так:
P (A × B) = P (A) × P (B|A)
Формула означает, что вероятность произведения двух событий равна произведению вероятности одного из них и условной вероятности другого, вычисленной при условии, что первое имело место (часть формулы, записанная как P (B|A), обозначает вероятность события B при условии, что событие A произошло). При этом:
- Событие А называется независимым от события B, если вероятность события А не зависит от того, произошло событие B или нет.
- Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.
Если мы имеем дело с независимыми событиями, то формула выглядит так:
P (A × B) = P (A) × P (В)

Задача: В миске лежат шарики: 2 оранжевых и 3 синих. Из миски вынимают подряд 2 шарика. Какова вероятность того, что оба шарика окажутся оранжевыми?
Решение: Обозначим извлечение двух оранжевых шариков подряд как событие A. Оно будет представлять собой произведение двух событий: A = A1 × A2, где:
A1 — это появление оранжевого шарика при первой попытке извлечения из миски,
A2 — это появление оранжевого шарика при второй попытке извлечения из миски.
P (A1) = 2/5
P (A2) = (2-1) / (5-1) = 1/4
P (A) = P (A1 × A2) = 2/5 × 1/4 = 0,1. Получается, что вероятность того, что оба шарика окажутся оранжевыми составляет всего 0,1, или 10 %.
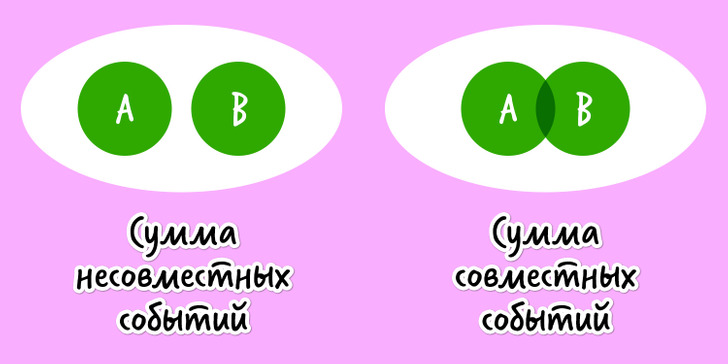
Суммой двух событий A и B называется такое событие A + B, при котором наступит или событие A, или событие B, или оба события одновременно. Если же события несовместны (то есть появление одного события исключает появление другого в рамках одного и того же испытания), то может наступить или событие A, или событие B.
Подбросив монетку, мы получим два противоположных и взаимоисключающих события: выпадет или орел, или решка. Когда два события противоположны друг другу, они обозначаются одинаковыми буквами, но над одной из них добавляется черточка или апостроф. К примеру, это будет А и Ā или А и А’.
Представьте, что у вас в пакете с фруктами лежат 9 груш: 4 зеленых, 3 красных и 2 желтых. Вы берете наугад одну из них. Какова вероятность того, что она не желтая?
Чтобы ответить на вопрос, нужно узнать вероятность того, что вы достанете зеленую грушу (А) и красную (В), а затем сложить их между собой (А + В), чтобы узнать, какова вероятность того, что вы достанете ту или другую (но не желтую).
P (A) = 4/9
P (B) = 3/9 = 1/3
Эти два события несовместны. Сложим их вероятности между собой:
P (A+B) = P (A) + P (B) = 4/9 + 1/3 = 7/9.
Получается, что вероятность того, что взятая груша будет не желтой составляет 7/9, или более 77 %.

Для решения этой задачи мы использовали формулу: P (A + B) = P (A) + P (B) из теоремы о сложении вероятностей, которая звучит так: «Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий».
Если мы имеем дело с совместными событиями (то есть появление одного события не исключает появление другого в рамках одного и того же испытания), то вероятность их суммы вычисляется по формуле: P (A + B) = P (A) + P (B) − P (A × B).
Все вышеуказанные формулы можно использовать, чтобы решать простые задачи по теории вероятностей.
Бонус: что означает фраза «вероятность дождя» в прогнозе погоды на самом деле?

Представьте, что в прогнозе погоды на завтра указано, что вероятность дождя составляет 30 %. Эта цифра кажется незначительной, и на следующий день вы отправляетесь на прогулку по городу без зонта, чтобы в итоге промокнуть до нитки. Как такое могло произойти, если вам обещали, что вероятность дождя составляет лишь 30 %?
Не спешите ругать метеорологов. Если вероятность дождя в прогнозе погоды для вашего города составляет 30 %, это говорит о 100%-й вероятности того, что дождь будет идти, но это произойдет лишь на 30 % территории города. Если в этот день вы будете перемещаться по городу, то для себя лично увеличите вероятность промокнуть.
