Как решать математические ребусы. 7 примеров с решениями

Математические ребусы представляют собой графические загадки, в которых зашифрованы числа и арифметические действия. Для решения обычно необходимо проявить в первую очередь логику и смекалку. Кроме того, развивается нестандартное мышление, ведь загадочную картинку можно интерпретировать по-разному в поисках ответа.

«Бери и Делай» подсказывает, как научиться быстро решать математические ребусы разной степени сложности.

Чем математические ребусы отличаются от обычных

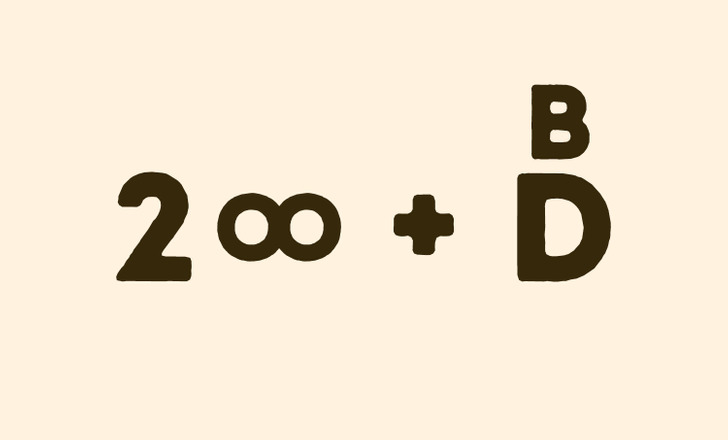
Ребус — это головоломка, где с помощью картинок и букв зашифровано слово или фраза. Некоторые лингвисты считают, что такого рода загадки легли в основу появления иероглифов в отдельных языках. А в XVIII–XIX веках люди часто использовали ребусы, чтобы шифровать отдельные слова в переписке.

Математический ребус — это тоже головоломка с картинками и цифрами. Но чтобы решить ее, нужно использовать математический подход или вспоминать алгебраический язык. К примеру, посмотрите на картинку выше. На ней зашифрована фраза на английском. Если произнести названия символов в порядке слева направо, то вы получите To (цифра 2, или two) + Infinity (символ бесконечности) + Beyond (буква B на D, или B on D) — To Infinity and Beyond, то есть «Бесконечность не предел».

Из этого можно сделать вывод о том, что любая картинка или символ в ребусе имеют какое-то значение для разгадки.

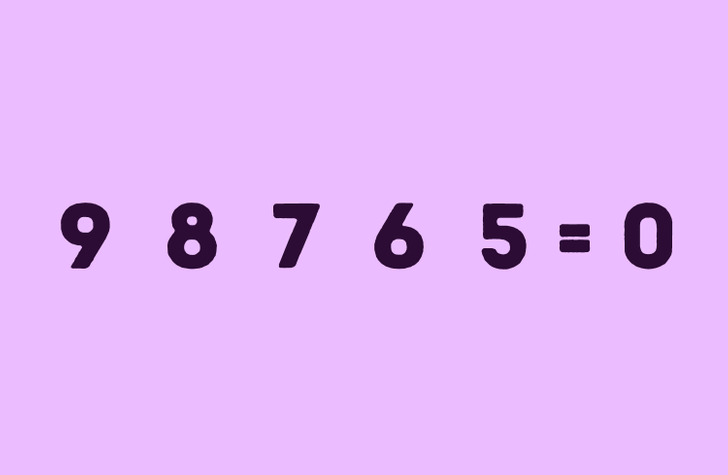
Получается, что для разгадки некоторых ребусов важно знать тот язык, на котором они составлены. Для решения ребуса выше достаточно знать 4 основных арифметических действия (сложение, вычитание, умножение и деление) и применить логическое мышление.

Итак, в левой части уравнения нужно расставить между цифрами математические знаки так, чтобы в результате получился ноль в правой части. Решение: 9 × 8 − 7 − 65 = 0.

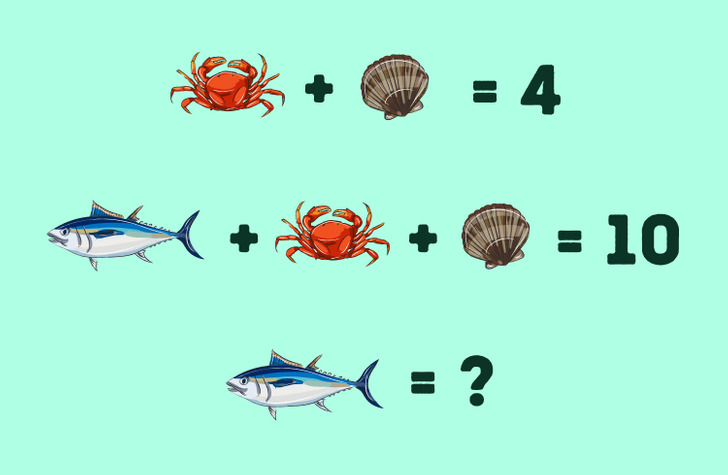
Ребус может скрывать в себе числовое выражение. На картинке выше зашифрована простая задача, в которой есть 2 уравнения с неизвестными. Чтобы решить ее, нужно учесть, что все уравнения связаны между собой, а за картинками скрываются целые числа, не равные нулю.

В 1-м выражении 1 краб и 1 ракушка в сумме дают 4. Это значит, что речь идет о двух разных слагаемых, которые в сумме дают 4. Их довольно просто найти: это 3 и 1. Чтобы узнать, чему равна рыба, нужно из суммы трех слагаемых вычесть сумму известных двух. Получается, 10 − 4 = 6. Следовательно, рыба равна 6.

Разобравшись с таким элементарным ребусом, можно переходить к тому, что посложнее.

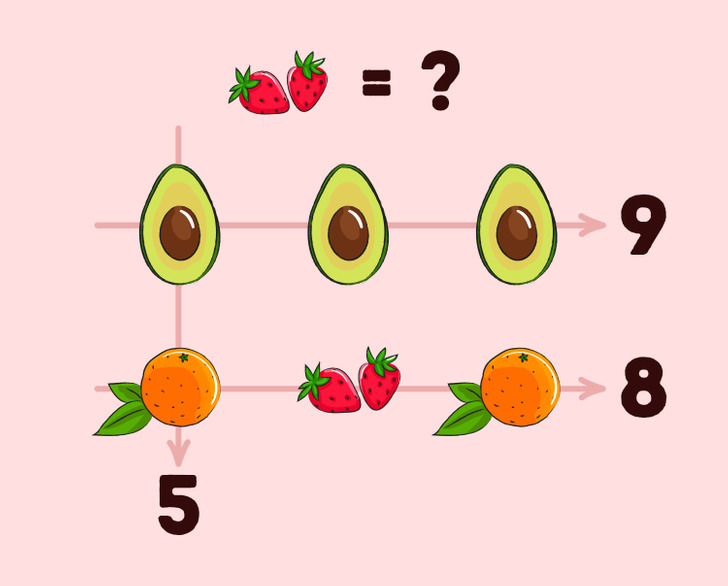
Такие загадки могут выглядеть по-разному. К примеру, на изображении выше представлена таблица с авокадо, клубникой и апельсином.

• Если сложить все авокадо в 1-м ряду, то в сумме будет 9.
• Если сложить ягоды и фрукты во 2-м ряду, получится 8.
• Если сложить авокадо и апельсин в 1-й колонке, то в сумме будет 5.

Нужно узнать, чему равна клубника. Эта задачка похожа на предыдущую, просто иначе проиллюстрирована и чуть сложнее. Решив ее правильно, в ответе вы получите 4: авокадо — это 3, а апельсин — это 2.

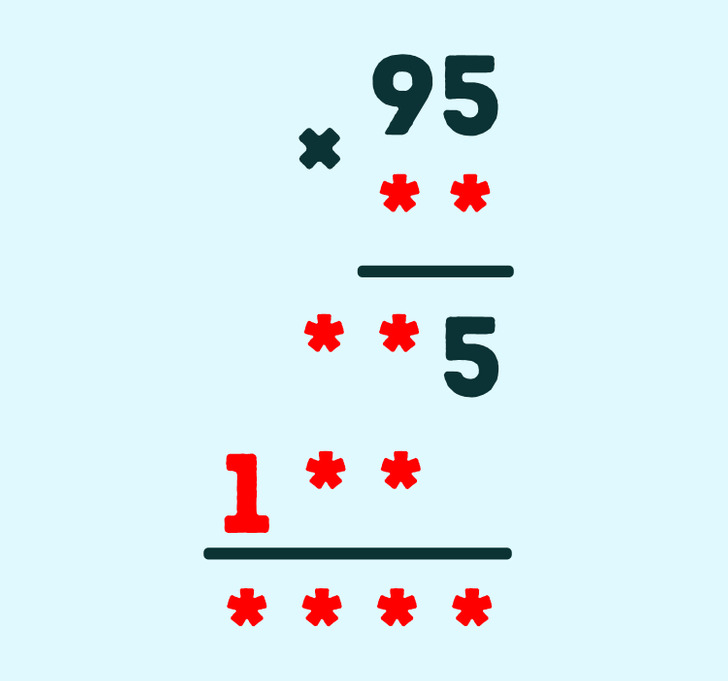
Математический ребус может выглядеть как обычный пример, где вместо привычных цифр проставлены точки или звездочки, как на картинке выше. В случае этого примера с умножением столбиком поможет метод подбора произведений и сумм, а также логическое мышление. Первые 2 звездочки — это число 23, затем идут 285 и 190, а последнее число — 2 185. Получается, 95 × 23 = 2 185.

Подобный ребус можно дополнительно усложнить, заменив числа буквами. На картинке выше зашифровано умножение двух 3-значных чисел столбиком. Разберем подробно его решение:

• Смотрим на 4-ю строку, где располагается результат умножения ABC × A. Если последняя цифра этого произведения равна A, то это не 1, иначе и C равнялось бы 1. При этом A не может быть больше 3, иначе в произведении было бы 4-значное число. Получается, что A = 2 или A = 3.
• Если A = 3, то C должно равняться 1. Но это неверно, так как ABC × С дает в 3-й строчке 4-значное число. Тогда A = 2 и при A × C должно получаться число, которое оканчивается на 2. Получается, C = 6.
• Смотрим на 5-ю строку, где находится результат умножения ABC × B, или 2B6 × B. Последняя цифра этого произведения равна B, и она же получается при 6 × B. Тогда за B может скрываться 4 или 8. В первом случае мы имеем 246 × 4 = 984, что не соответствует 4-значному произведению. Получается, B = 8.

В итоге имеем, что A = 2, B = 8, C = 6. Следовательно, 286 × 826 = 236 236. В 3-й строчке получаем 1 716, в 4-й строке получаем 572, в 5-й строке — 2 288. Ребус решен.

Бонус: простая загадка, которую многие решают очень быстро, но неправильно

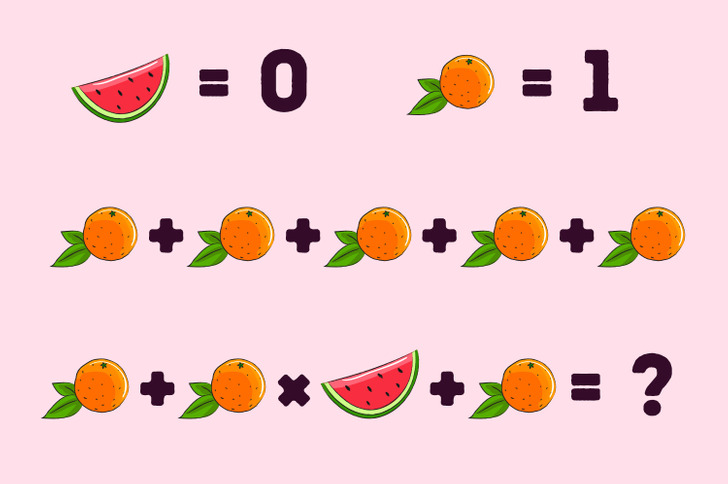
Посмотрите на картинку выше и постарайтесь решить пример как можно быстрее. Скорее всего, вы допустите ошибку. Почему?

Если заменить апельсины и арбуз числами, то получится 1 + 1 × 0 + 1 = 2. Возможно, у кого-то при расчетах получилось 7, потому что учитывалась 1-я строчка. На самом деле если бы все апельсины и арбузы были частью одного выражения, то 2-я строчка начиналась бы с плюса. Поэтому здесь нужно складывать и умножать лишь то, что находится во 2-й строке.