Почему нельзя делить на ноль

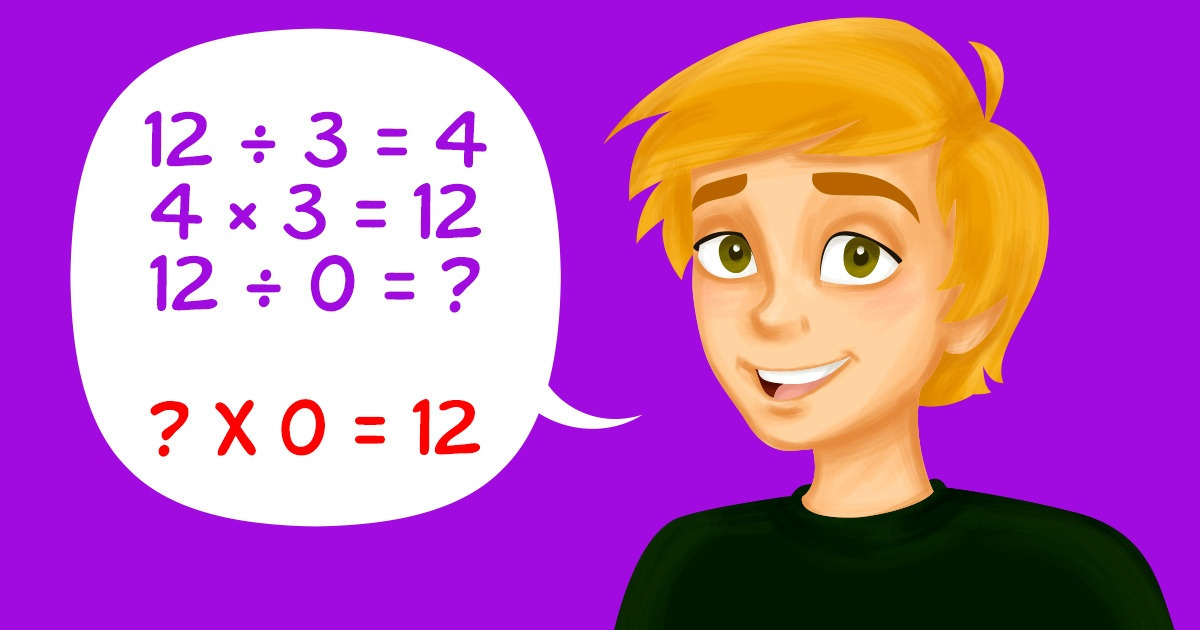
В школе нас учили, что делить на 0 нельзя. Существуют даже шутки о том, что черные дыры появились потому, что кто-то пытался это сделать. Но как дела обстоят на самом деле?

Мы в «Бери и Делай» решили подойти к вопросу обстоятельно и наконец выяснить, что будет, если нарушить это заветное табу.

Что такое деление

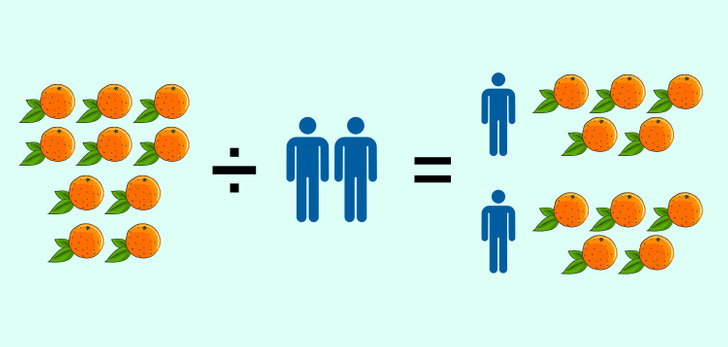
На простом арифметическом уровне деление подразумевает разделение группы объектов на равные части. Например, возьмем 10 апельсинов, которые нужно поделить между 5 людьми, сидящими за столом. Каждый человек получит количество фруктов, равное 10 ÷ 5, то есть 2. Если бы за столом сидел 1 человек, то ему досталось бы 10 ÷ 1, то есть 10 апельсинов.

Возникает вопрос: сколько из 10 апельсинов достанется каждому, если за столом сидит 0 человек?

Почему нельзя делить на 0

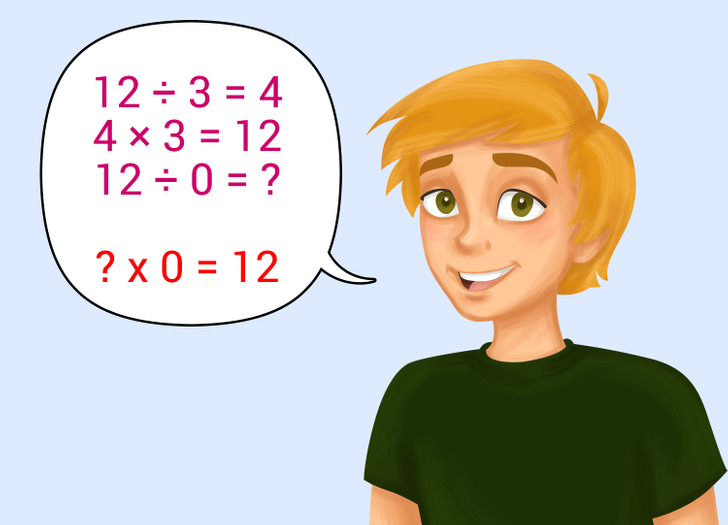
Дело в том, что деление на 0 не имеет смысла, так как любые попытки это сделать приводят все к новым и новым противоречиям. Приведем пример.

Как правило, после деления мы можем вернуться назад, используя умножение. Для уравнения r = a ÷ b должно быть верно a = r × b.
Если допустить, что b = 0, то у нас получится r × 0 = a.

Если 12 ÷ 3 = 4, то 4 × 3 = 12.
Если 12 ÷ 0 = ?, то мы, казалось бы, должны получить ? × 0 = 12.

Но так как любое число, умноженное на 0, равняется 0, то мы должны получить r × 0 = 0.
Выходит, что при любом значении r, если a ≠ 0, уравнение нельзя решить.

А что насчет бесконечности?

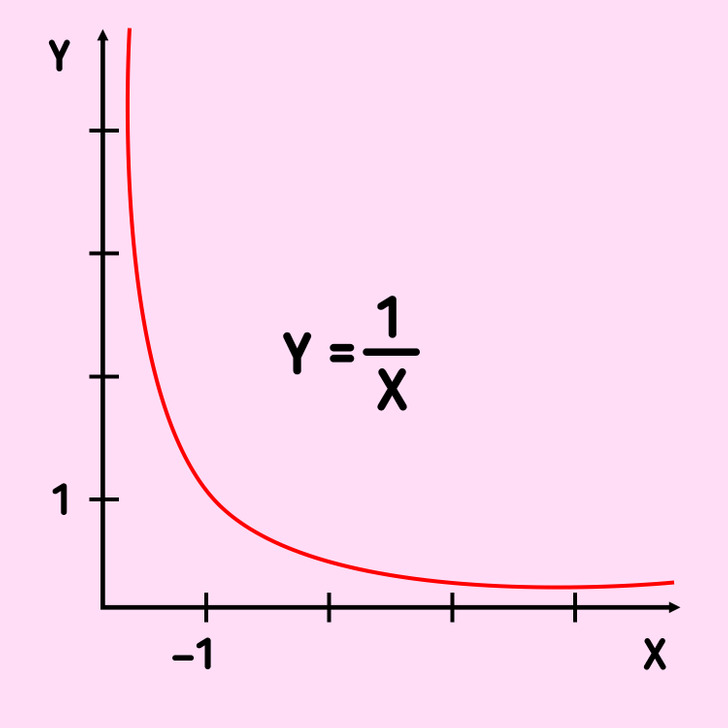
Можно предположить, что дробь, знаменатель которой 0, равняется бесконечности. Эта мысль не лишена логики. Возможно, вы замечали, что при делении числа на все меньшее и меньшее число мы получаем все большее и большее число. Для наглядности приведем пример:

20 ÷ 5 = 4

20 ÷ 2 = 10

20 ÷ 0,5 = 40

20 ÷ 0,0000005 = 40 000 000

Можно заметить, что делитель бесконечно уменьшается, а частное бесконечно растет, тем самым стремясь к бесконечности. Однако стремиться к бесконечности и быть равным бесконечности — 2 совершенно разных понятия. Ведь бесконечность — это не конкретное число, а скорее абстрактная идея. Если бы мы попробовали отнестись к бесконечности как к числу (например, в уравнении 1 : 0 = ∞), то мы столкнулись бы со следующими математическими аномалиями:

1 ÷ 0 = ∞ = 2 ÷ 0
1 = 0 × ∞ = 2
Соответственно,
1 = 2

При таком раскладе мы получили бы утверждение, что все целые числа равны друг другу, и вся система рухнула бы.

А что, если разделить 0 на 0?

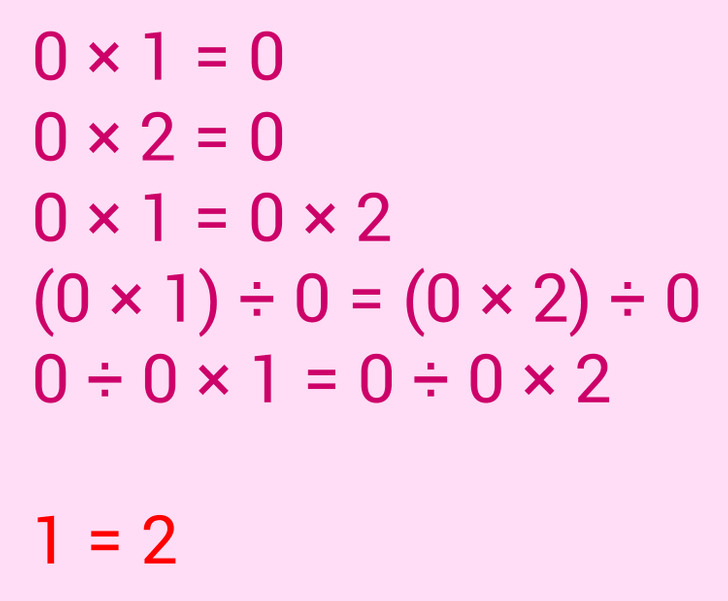
Попробуем рассмотреть еще один пример.

Допустим, что
0 × 1 = 0
0 × 2 = 0
Тогда верно следующее:
0 × 1 = 0 × 2
Деление обеих частей на 0 дает:
(0 × 1) ÷ 0 = (0 × 2) ÷ 0
0 ÷ 0 × 1 = 0 ÷ 0 × 2
Проще говоря,
1 = 2

Ошибка здесь состоит в предположении, что при делении 0 на 0 действуют те же правила, что и при делении на другие числа.

Если подвести итог всего вышесказанного, то правило «На 0 делить нельзя» становится понятнее: на 0 делить нельзя не потому, что произойдет что-то критичное, а потому, что это просто-напросто не имеет смысла.