Как решать квадратные уравнения

Решение квадратных уравнений — это важная тема в школьном курсе алгебры. Если хотите освежить знания, помочь подросткам с уроками или впервые знакомитесь с этим вопросом, воспользуйтесь нашей простой инструкцией, где собраны несколько способов решения квадратных уравнения.

Мы в «Бери и Делай» постарались максимально просто и понятно объяснить эту тему, а в конце статьи добавили бонус, благодаря которому вы сможете за секунды решать подобные уравнения.

Что такое уравнение

Уравнение — это равенство, где есть переменная, чье значение нужно найти. Выражение 3 + x = 9 — это уравнение с переменной x. Именно ее значение нужно найти.

Корнем уравнения называют такое значение переменной, при подстановке которого уравнение превращается в верное равенство. Если в вышеуказанное уравнение мы подставим вместо x число 5, то получим 3 + 5 = 8, что противоречит правой части уравнения. Если вместо x взять число 6, то получим 3 + 6 = 9, а значит, 6 является корнем уравнения.

Решая уравнения, мы ищем все его корни или доказываем, что их не существует.

Что такое квадратное уравнение

Это уравнение вида ax² + bx + c = 0, где корнем является значение переменной x, обращающее квадратный трехчлен в 0, а само квадратное уравнение — в верное равенство. Другими словами, благодаря наличию x² это уравнение является квадратным.

Квадратное уравнение содержит коэффициенты:

• а — старший или первый коэффициент, не равный 0 (иначе это линейное уравнение)
• b — второй коэффициент
• c — свободный член

Не всегда новичкам легко определить коэффициенты уравнения, потому что b и c вместе или по отдельности могут равняться 0. Обратите внимание, как могут выглядеть квадратные уравнения и их коэффициенты:

О чем важно знать:

• В уравнении x² + 7x + 1 = 0 старший коэффициент равен 1. Такие квадратные уравнения называются приведенными. Если старший коэффициент отличается от 1, например равен 2, как в примере 2ײ + 7x + 1 = 0, то это неприведенное квадратное уравнение.
• По условию в квадратном уравнении a ≠ 0. Но другие коэффициенты могут равняться 0, например x² + 5x = 0, или 5ײ = 0, или x² + 5 = 0. Если коэффициенты b и c равны по отдельности или вместе 0, то квадратное уравнение называется неполным. Соответственно, у полного квадратного уравнения все коэффициенты отличны от нуля.
• Как привести уравнение к виду ax² + bx + c = 0? Допустим, у нас есть уравнение x² — 3x — 5 = 11 — 3x. В этом случае нужно сделать так, чтобы в правой части остался только 0: x² — 3x — 5 — 11 + 3x = 0. Полученное уравнение можно сократить до x² — 16 = 0. Получилось приведенное неполное квадратное уравнение, где коэффициенты а = 1, b = 0, c = —16.

Как решать неполные квадратные уравнения

Существует 3 типа неполных квадратных уравнений:

• ax² = 0, где коэффициенты b = 0 и c = 0
• ax² + c = 0, при b = 0
• ax² + bx = 0, при c = 0

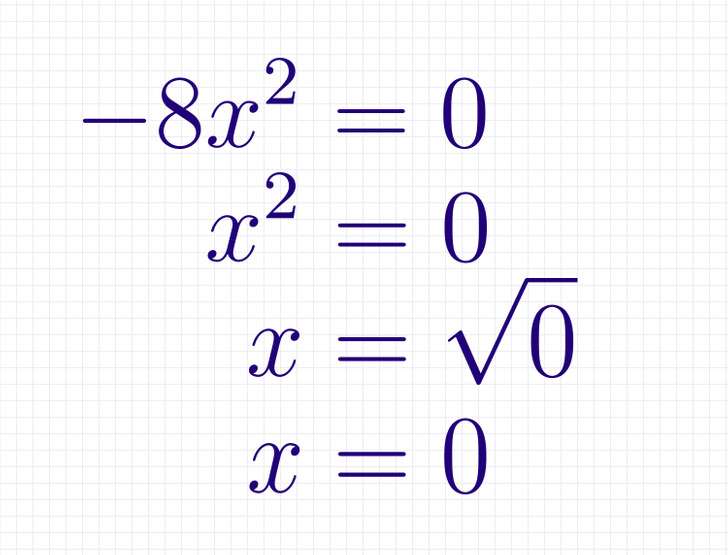
• Как решить уравнение типа ax² = 0

У этого уравнения коэффициенты b и c равны 0, но а ≠ 0. Если уравнение ax² = 0 разделить на некое число a (которое по условию не равняется 0), то получим x² = 0. Получается, что корнем уравнения является 0, так как 0² = 0. Других корней у уравнения нет. Значит, любое неполное квадратное уравнение ax² = 0 имеет только один корень x = 0.

На картинке выше в качестве примера мы решили уравнение —8ײ = 0 и выяснили, что корень x = 0.

Вывод: уравнение типа ax² = 0 имеет только один корень x = 0.

• Как решить уравнение типа ax² + с = 0

В этом типе уравнения b = 0, но c ≠ 0 и а ≠ 0. Преобразуем уравнения, перенеся свободный член в правую часть: ax² = —c. Теперь разделим обе части на первый коэффициент a и получим x² = —c/а.

Если c/а < 0, то уравнение x² = —c/а не имеет корней, потому что квадрат любого числа равен неотрицательному числу. Если же c/а > 0, то уравнение имеет 2 корня.

На картинке выше мы решили уравнение 8ײ + 5 = 0, выяснив, что у него нет корней.

Вывод: уравнение типа ax² + с = 0 не имеет корней или имеет 2 корня, которые при возведении в квадрат дают x² = —c/а.

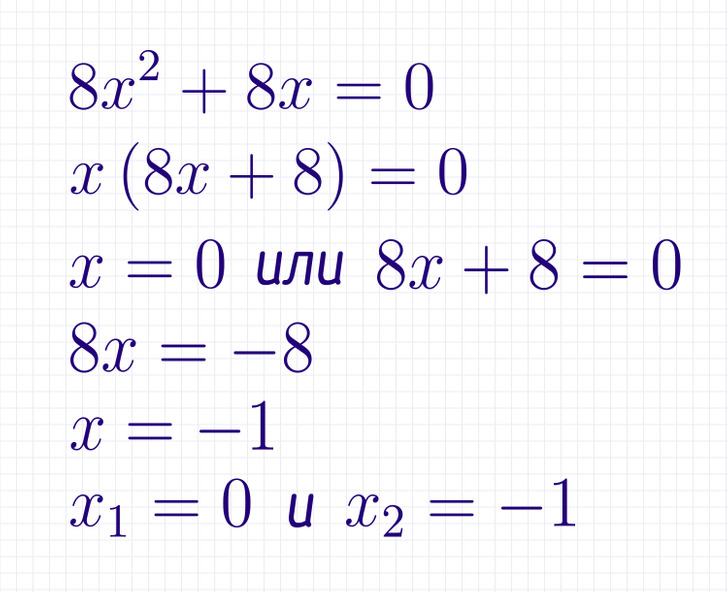
• Как решить уравнение типа ax² + bx = 0

В таком типе уравнения c = 0, но а ≠ 0. Чтобы решить его, можно использовать метод разложения на множители. Возьмем многочлен в левой части и разложим его на множители, убрав за скобки общий множитель х. Получим: x × (ax + b) = 0. Отсюда получаем, что х = 0 или ax + b = 0. Во втором случае мы имеем уже линейное уравнение, чей корень равен x = −b/a. Получается, что у уравнения ax² + bx = 0 имеется 2 корня: x₁ = 0 и x₂= −b/a.

На картинке выше мы решили уравнение 8ײ + 8x = 0, определив два корня: x₁ = 0 и x₂ = −1.

Вывод: уравнение типа ax² + bx = 0 имеет 2 корня, это x₁ = 0 и x₂= −b/a.

Что такое дискриминант и формула для нахождения корней

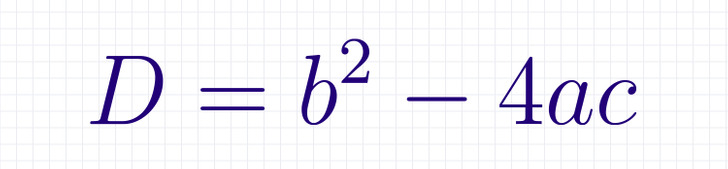
Определить количество корней квадратного уравнения можно и не решая его, с помощью выражения дискриминанта (обозначается буквой D), в которое подставляют коэффициенты квадратного уравнения.

Свойства дискриминанта подскажут, сколько корней имеет уравнение:

• если D < 0, корней нет
• если D = 0, то есть один корень. Вычислить его можно по формуле х = −b/2a
• если D > 0, то есть 2 различных корня. В этом случае их можно вычислить по формуле:

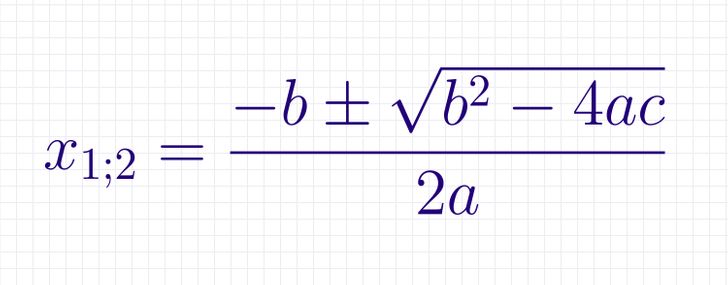
Обратите внимание, что в этой формуле тоже есть дискриминант, он находится под корнем. Это универсальная формула для нахождения корней квадратного уравнения. Как ею пользоваться?

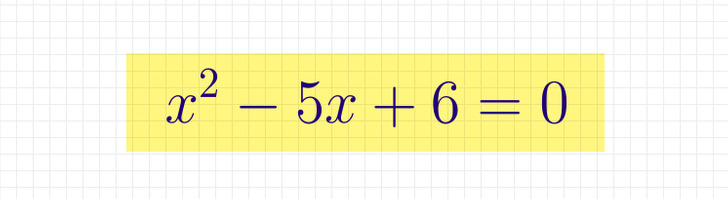
Допустим, нужно вычислить корни уравнения x² — 5x + 6 = 0.

Шаг № 1: Запишем квадратное уравнение и определим его коэффициенты. В данном случае мы имеем: a = 1, b = —5, c = 6. Вычислим значение дискриминанта по формуле D = b² — 4ac. Получим, что D = 1. Получается, у нашего уравнения 2 корня.

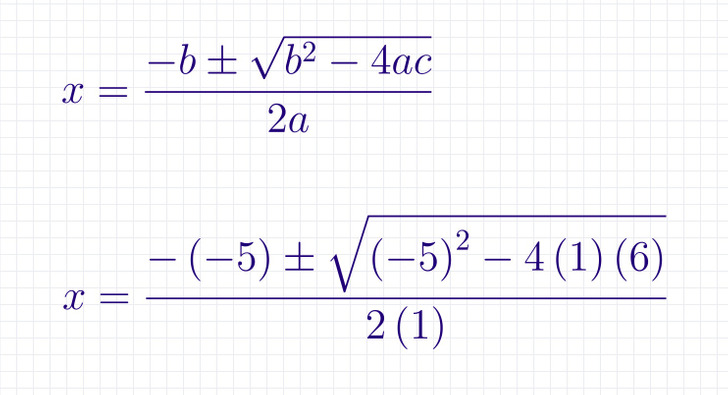
Шаг № 2: Найдем корни уравнения через формулу с дискриминантом, подставив в нее коэффициенты.

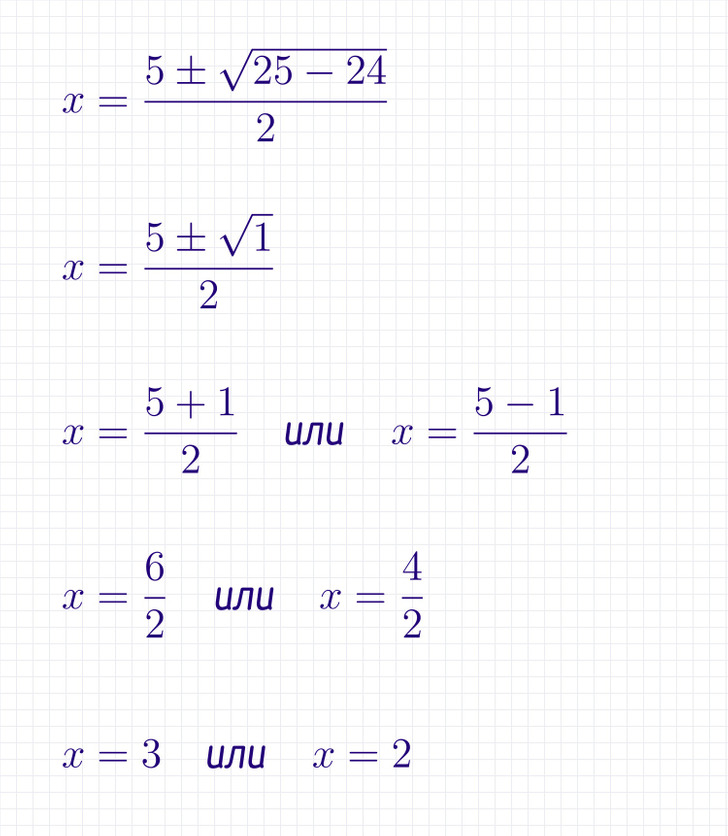
Шаг № 3: Произведем вычисления и получим значения двух корней. Получаем, что уравнение x² — 5x + 6 = 0 имеет 2 корня: x₁ = 3 и x₂ = 2. Готово!

Как решить квадратное уравнение, разложив его на множители

Мы уже пользовались этим способом выше, когда решали неполное уравнение типа ax² + bx = 0. Разложить на множители можно любое квадратное уравнение, но этим стоит заниматься только в том случае, если это облегчит расчеты.

Например, попробуем решить уравнение х² + 10х — 24 = 0. Сначала разложим левую часть на множители и получим х² + 10х — 24 = х² + 12х — 2х — 24 = х(х + 12) — 2(х + 12) = (х + 12)(х — 2). Теперь наше уравнение можно записать как (х + 12)(х — 2) = 0. Получается, что хотя бы один из множителей равен нулю. Если (х + 12) = 0, то х = —12. Если (х — 2) = 0, то х = 2.

Тогда уравнение х² + 10х — 24 = 0 имеет 2 корня: x₁ = −12 и x₂ = 2.

Как быстро решать квадратные уравнения с помощью теоремы Виета

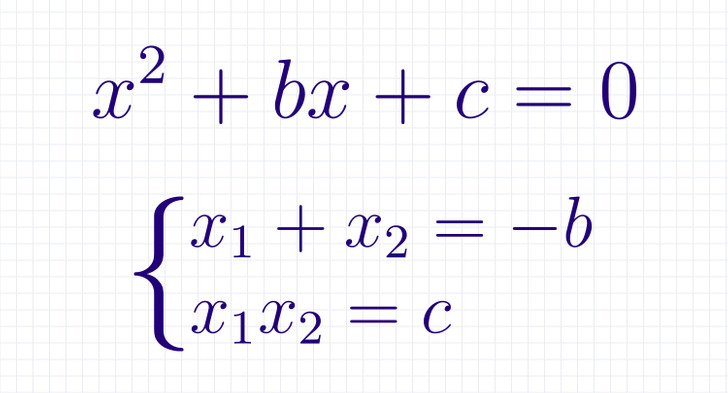
Согласно теореме Виета, сумма корней x₁ и x₂ в уравнении x² + bx + c = 0 равна второму коэффициенту с противоположным знаком, а произведение этих же корней равняется свободному члену или c (мы изобразили это на картинке выше). Другими словами, получается, что корни уравнения фактически спрятаны внутри коэффициентов уравнения.

Благодаря этому, если вы имеете дело с приведенным квадратным уравнением (у которого a = 1), то эта теорема может помочь вам быстро найти корни уравнения.

В качестве примера возьмем уравнение x² — 8x + 15 = 0. Это приведенное квадратное уравнение (т. е. старший коэффициент равен 1), а D = 4, а значит, корня точно 2. Воспользуемся теоремой Виета и получим следующие равенства:

x₁ + x₂ = 8

x₁ × x₂ = 15

Нам надо найти такие 2 числа, которые в сумме дают 8, а их произведение равно 15. Методом подстановки получаем x₁ = 3 и x₂ = 5. На всякий случай проверим, решив уравнение с помощью формулы для нахождения корней. Подставим коэффициенты в формулу, произведем вычисления и получим: х₁ = (8 — 2) / 2 = 3 и x₂ = (8 + 2) / 2 = 5. Все верно!

Важно: использовать теорему Виета следует в тех случаях, когда это облегчит расчеты.

Бонус: хитрость, которая позволяет быстро находить корни квадратного уравнения

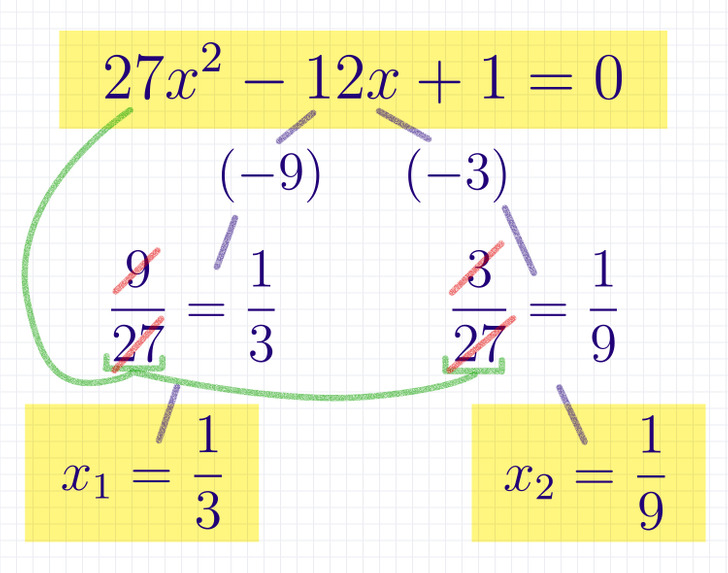
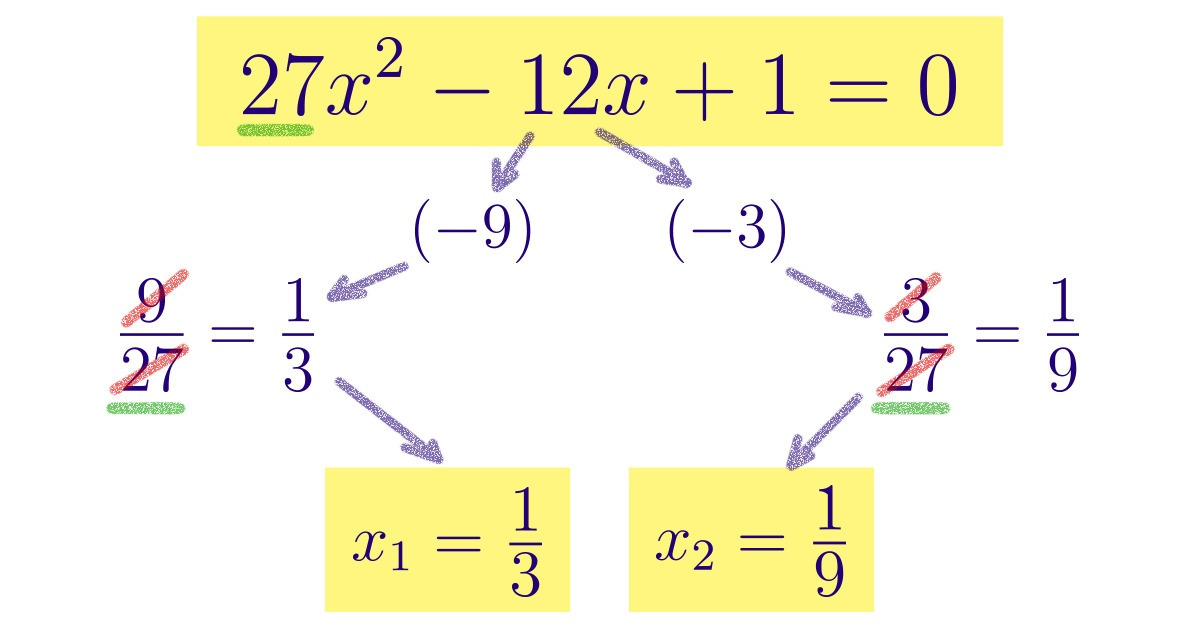
Попробуем пошагово быстро решить квадратное уравнение 27ײ — 12х + 1 = 0 с помощью этой хитрости:

Шаг № 1: В уравнении 27ײ — 12х + 1 = 0 обратим внимание на второй коэффициент, который равен —12.

Шаг № 2: Подберем 2 таких числа, которые в сумме дают —12. При этом их произведение должно равняться числу 27, которое является произведением a и с, т. е. это 27 × 1 = 27. В нашем случае это числа —9 и —3.

Шаг № 3: Теперь поменяем у этих чисел знаки на противоположные, получив 9 и 3. И разделим каждое из них на число первого коэффициента уравнения, т. е. в нашем случае на 27. Получим 2 числа: это 9/27 и 3/27. Эти числа можно сократить, получив 1/3 и 1/9. Они и являются корнями уравнения, т. е. уравнение 27ײ — 12х + 1 = 0 имеет 2 корня: x₁ = 1/3 и x₂ = 1/9. На всякий случай можно проверить себя, решив уравнение с помощью формулы для нахождения корней.