Как складывать и вычитать обыкновенные дроби

Дробь — это число, состоящее из одной или нескольких частей единицы. Она состоит из числителя, который показывает, сколько частей мы имеем, и знаменателя, который показывает общее количество частей, на которое разделено целое.

«Бери и Делай» покажет, как выполнять действия с общими и разными знаменателями.

Части дроби

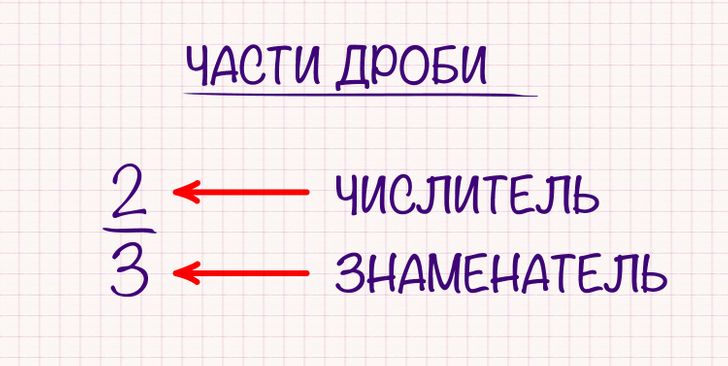
• Числитель — количество частей, которое у нас есть
• Знаменатель — общее количество частей

Типы дробей

• Правильная дробь — числитель меньше знаменателя
• Неправильная дробь — числитель больше знаменателя
• Смешанная дробь состоит из целого числа и правильной дроби

Дроби с общим знаменателем

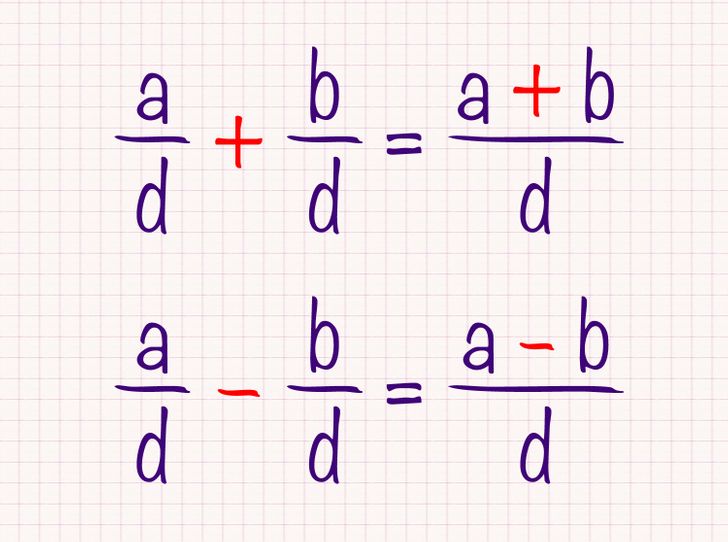
Для решения задач с дробями с общим знаменателем числители складываются или вычитаются как обычно, а знаменатель остается неизменным.

Сложение и вычитание дробей с общим знаменателем

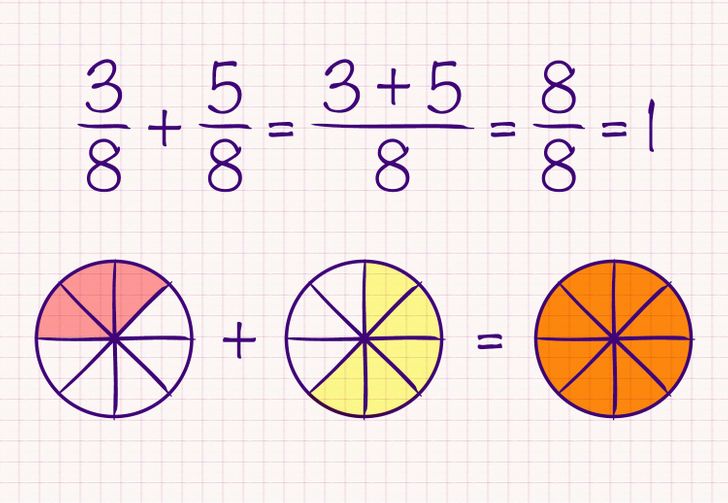
Возьмем для примера дроби 3/8 и 5/8.

• Сложим числители 3 + 5 и оставим знаменатель 8. Ответ будет 8/8. После упрощения получим окончательный результат 1.

Для вычитания возьмем дроби 5/7 и 3/7

• Для вычитания дробей с общим знаменателем делаем то же самое. Просто вычитаем один числитель из другого (3 из 5) и оставляем знаменатель неизменным. В результате получаем 2/7.

Дроби с разными знаменателями

Существует 2 способа решения задач с дробями, не имеющими общего знаменателя. Первый способ называется «наименьшее общее кратное», а второй — «умножение крест-накрест».

Наименьшее общее кратное

Первый способ заключается в нахождении наименьшего общего кратного числа для двух знаменателей.

Для примера возьмем знаменатели 4 и 6. Будем умножать их попеременно на каждое число начиная с 1 (затем 2, 3 и т. д.) до тех пор, пока не найдем общий результат для обоих (это и будет наименьшее общее кратное). Для нашего случая наименьшее общее кратное равно 12. Мы видим, что 24 также является общим кратным, но не является наименьшим.

Сложение дробей с вычислением наименьшего общего кратного

Для примера сложим дроби 9/12 и 5/8.

• Находим наименьшее общее кратное для знаменателей 12 и 8, записав результаты их умножения на разные числа в 2 столбика. В нашем примере таким числом будет 24.
• Затем делим 24 на первый знаменатель и результат умножаем на первый числитель.
• Повторяем этот шаг для второй дроби. Сумма двух полученных чисел будет числителем в нашем ответе. А знаменателем будет найденное нами наименьшее общее кратное.

Примечание: Вы можете упростить полученную дробь, если можно разделить числитель и знаменатель на одно и то же число. Иногда в результате получается целое число.

Сложение дробей путем умножения крест-накрест

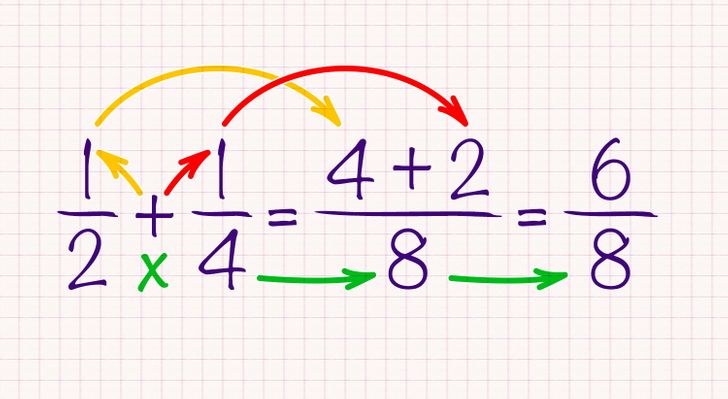
Допустим, нам нужно вычислить 1/2 + 1/4. Как действовать:

1. Умножаем один знаменатель на другой и используем результат в качестве общего знаменателя. В нашем случае это 8.
2. Затем умножаем второй знаменатель на первый числитель и ставим результат на первое место над общим знаменателем в новой дроби после знака равенства.
3. Вторым числом, которое мы запишем над общим знаменателем в новой дроби, будет результат умножения первого знаменателя на второй числитель.
4. В окончательном ответе в знаменателе будет сумма этих двух чисел, а в числителе — результат первого умножения.