Как вычислить квадратный корень вручную

Если число умножить на само себя, то результат этого действия будет называться квадратом этого числа. Например, 3 × 3, или 3², равняется 9, где число 9 является квадратом числа 3. Обратное действие, когда надо узнать, какое число, возведенное в квадрат, даст число 9, называется извлечением квадратного корня. Хоть это кажется сложным и несколько утомительным, зная алгоритмы решения, вы легко справитесь с подобной задачей.

«Бери и Делай» предлагает познакомиться с несколькими способами извлечения квадратного корня, которые могут пригодиться не только в школе, но и в реальной жизни.

Что полезно знать об извлечении квадратного корня

Извлечение арифметического квадратного корня похоже на действие, обратное возведению числа во вторую степень, или в квадрат. Но это не совсем так. К примеру, если неотрицательное число (a) и равное ему по модулю отрицательное число (—a) возвести в квадрат, то в результате получится одно и то же неотрицательное число. При попытке совершить обратное действие мы не сможем восстановить знак числа и определить, возводилось ли в квадрат отрицательное или неотрицательное число, мы будем знать лишь модуль числа. Поэтому из определения квадратного корня для любого действительного числа справедливо равенство:

√a² = |a|

То, что находится под знаком корня, называется подкоренным числом, или выражением. В примере выше справа от знака равенства находится модуль числа a. Далее мы отталкиваемся от того, что извлечь квадратный корень можно только из положительного числа. При этом если a ≥ 0, то (√a)² = a.

Важно: Могут быть ситуации, в которых важна двузначность корня. Тогда перед его знаком ставится знак ± (плюс-минус), например так делается в формуле решения квадратного уравнения.

Квадратный корень нуля и единицы

Существует несколько простых правил, которые легко запомнить:

• Квадратный корень из нуля равен нулю.
• Квадратный корень из единицы равен единице.
• Квадратный корень из отрицательного числа извлечь нельзя (но есть исключение — если вы работаете с мнимыми числами).

Как извлечь корень из чисел, квадраты которых известны

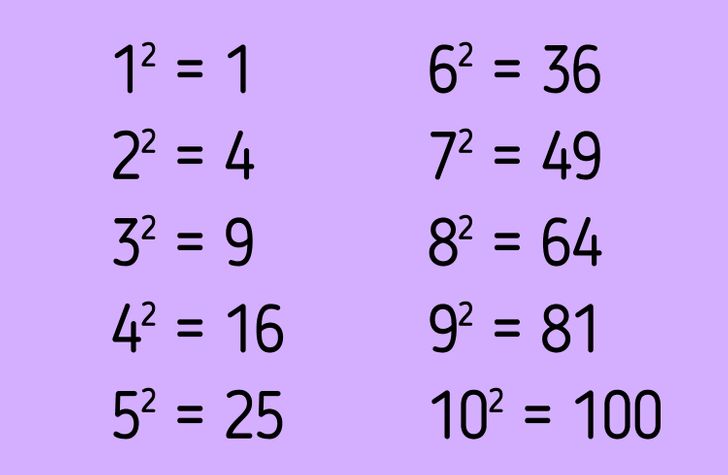
Для некоторых чисел квадраты известны, поэтому их можно всегда посмотреть в соответствующей таблице, а какие-то (наиболее используемые в том или ином случае) даже выучить наизусть. Например, зная таблицу умножения, вы без проблем извлечете квадратный корень из любого числа до 100, если этот корень извлекается нацело или без остатка (как на картинке выше).

При этом такой квадрат называется полным, или точным. Например, если число 2 возвести в квадрат, то получится число 4, которое является полным, или точным, квадратом числа 2. Соответственно, большую трудность представляет вычисление квадратного корня из числа, которое не является полным квадратом. Также есть числа, из которых невозможно извлечь корень, например √2, можно лишь обнаружить приближенное значение. При работе с квадратными корнями, которые извлекаются нацело и кажутся достаточно простыми, тоже могут возникнуть сложности.

Пример № 1: Необходимо вычислить √0,09.

Число 0,09 является десятичной дробью. Но мы можем забыть об этом и представить ее в виде целого числа 9. Далее мы вспоминаем, что число 9 получается, если взять число 3 в квадрате. Тогда √9 = 3. Далее вспоминаем правило умножения десятичных дробей: количество знаков после запятой в результате умножения десятичных дробей будет равняться сумме количества знаков после запятой каждой дроби. Тогда при вычислении √0,09 (где после запятой два знака) нам нужно найти такую десятичную дробь, у которой будет только один знак после запятой. Получается, что ответ — это 0,3. Проверим, умножив 0,3 на само себя, и получим в результате 0,09. Значит, √0,09 = 0,3.

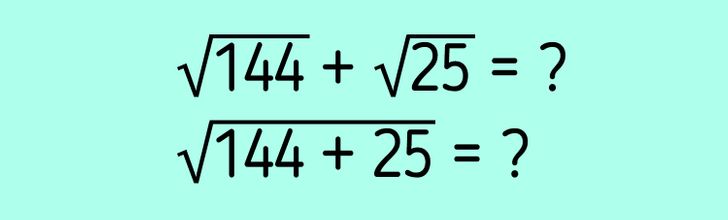
Пример № 2: На картинке выше записаны два примера. Как вы думаете, в результате получается одно и то же число или два разных?

В первом примере под одним корнем одно число, под другим — другое. Мы не можем их сложить между собой, а затем вычислить корень (складывать или вычитать можно только одинаковые квадратные корни, при этом работа ведется только с множителями, которые стоят слева от корня, а само подкоренное выражение не изменяется). Необходимо вычислить корень для каждого конкретного числа, а затем сложить результаты. В этом случае мы имеем дело с полными квадратами, поэтому легко вычислить, что √144 = 12, а √25 = 5. Теперь складываем полученные числа и получаем результат первого примера: 12 + 5 = 17.

Во втором примере под одним корнем находится выражение. Чтобы вычислить квадратный корень, сначала надо упростить выражение, выполнив действие сложения под корнем: 144 + 25 = 169. Теперь из числа 169 мы извлекаем квадратный корень и получаем 13.

Таким образом, в результате решения каждого примера получаются разные числа.

Вычисление квадратного корня через разложение на простые множители

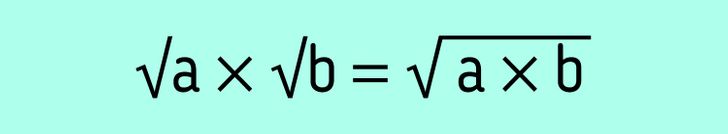
Согласно правилу, чтобы умножить один квадратный корень на другой, нужно перемножить их подкоренные выражения, а результат записать под общим знаком корня (при условии что подкоренные выражения или числа больше или равны нулю). Получается, чтобы вычислить квадратный корень из числа, мы можем разложить подкоренное число на простые множители, а затем произведение представить в виде степени с нужным показателем и извлечь корень.

На картинке выше число 3 136 мы разложили на простые множители. Таким образом, корень из этого числа будет равен корню, под которым будет выражение 2² × 2² × 2² × 7². Зная, что по свойству квадратного корня (√a)² = a, мы можем упростить выражение до 2 × 2 × 2 × 7 = 56. Таким образом, квадратный корень из 3 136 равняется 56.

Главный минус этого способа в том, что число не всегда можно разложить до конца и это занимает много времени.

Метод вычета нечетного числа

Этот метод основан на том, что квадрат натурального числа n можно представить в виде суммы первых n нечетных чисел, например:

1² = 1
2² = 1 + 3 = 4
3² = 1 + 3 + 5 = 9
4² = 1 + 3 + 5 + 7 = 16

Тогда при вычислении квадратного корня из числа можно вычитать нечетные числа по порядку, пока остаток не станет меньше следующего вычитаемого числа или не окажется равен нулю. После этого нужно посчитать количество операций — это число и будет целой частью числа извлекаемого квадратного корня.

Пример: Необходимо вычислить √16.

Сначала вычтем из числа нечетные числа по порядку:

16 — 1 = 15
15 — 3 = 12
12 — 5 = 7
7 — 7 = 0

Мы получили ноль, что означает, что корень извлекается нацело. Теперь посчитаем количество действий. Выполнено 4 действия, значит, √16 = 4.

Основным минусом данного способа является то, что он удобен только в случае с небольшими числами.

Вычисление квадратного корня уголком или столбиком

Этот способ позволяет извлечь квадратный корень из любого числа с высокой точностью, но может показаться достаточно сложным, если в ответе число состоит из большого количества цифр. Ниже один из вариантов его записи на бумаге.

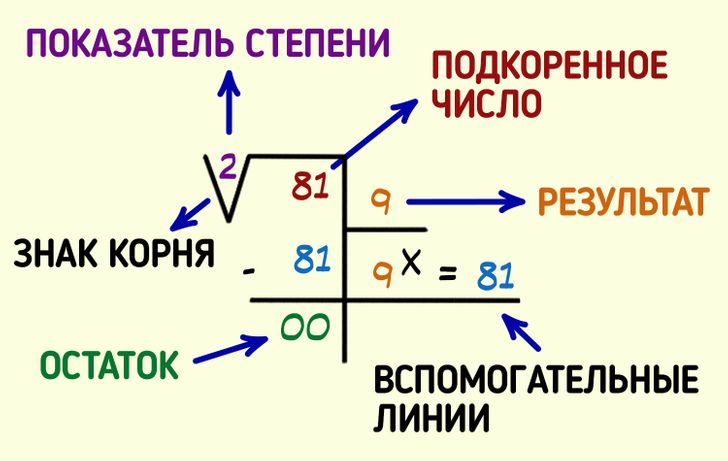
На картинке выше изображены следующие элементы:

• Знак корня указывает, что производится вычисление квадратного корня.
• Показатель степени, который будет равен 2, если вам нужно найти квадратный корень, и в таком случае его необязательно обозначать цифрой.
• Подкоренное число, или выражение, из которого извлекается квадратный корень.
• Результат — место, где записывается конечный результат всей операции.
• Вспомогательные линии — строки, где выполняются математические действия, приводящие к окончательному решению задачи.
• Остаток — сумма, которая может остаться после завершения вычислений, если корень извлекается не нацело.

Выше в качестве примера показано извлечение квадратного корня из числа 81. Чтобы лучше объяснить весь процесс, возьмем в качестве примера натуральное число 50 419 и попытаемся найти его квадратный корень.

1. Разделите цифры подкоренного числа на пары, двигаясь справа налево. В этом конкретном примере число состоит из 5 цифр, а значит, и самая левая из них, пятерка, остается без пары.

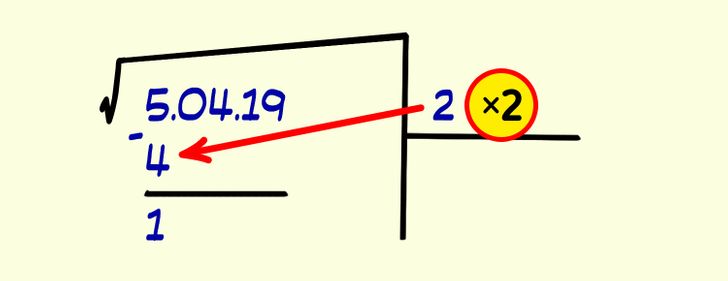
2. Найдите число, которое при умножении на само на себя даст результат, максимально приближенный к первой цифре подкоренного числа (но не больше ее). Запишите это число в строку результата справа. Затем вычтите полученный результат из первой цифры подкоренного числа и запишите ответ.

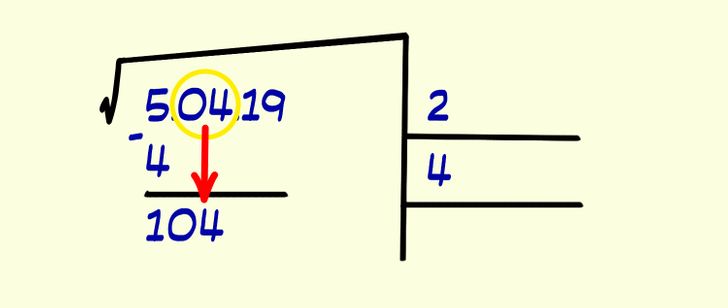
3. Перенесите следующие 2 цифры подкоренного числа (в данном случае это цифры 0 и 4), записав их рядом с остатком от вычитания. В данном случаем мы получим число 104.

Теперь найденное число, записанное в строке результата справа вверху (2), умножаем на 2, получаем число 4 и записываем его в строке ниже.

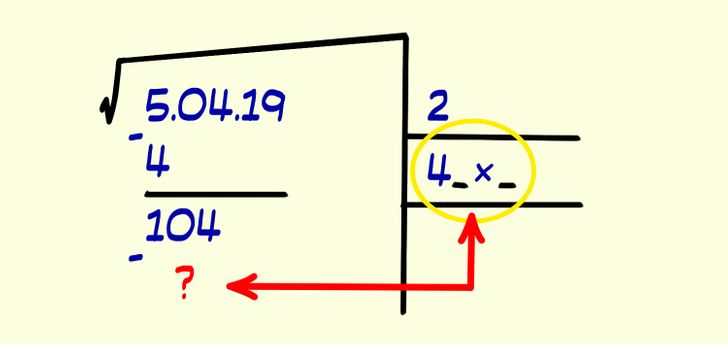
4. Теперь справа от полученного числа 4 нужно записать выражение. Для этого найдите такое целое число, чтобы после того, как вы его подставите в правое выражение 4_ × _, результат был равным или максимально приближенным к числу остатка (104), но не превышал его.

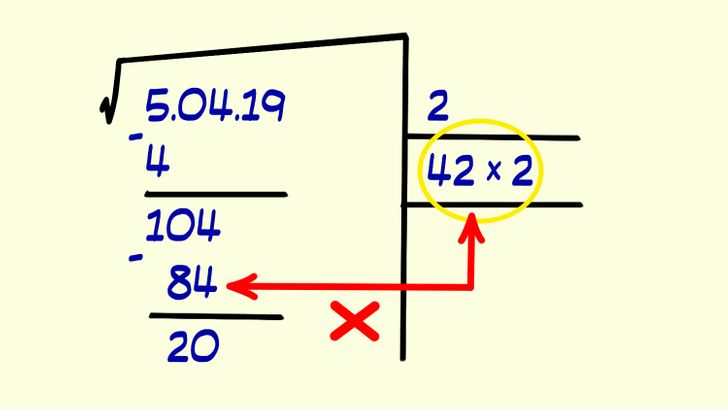
В данном случае лучше всего подойдет двойка, потому что тогда мы получим 42 × 2 = 84, то есть число, которое меньше 104. Если взять тройку, то 43 × 3 = 129, а это число уже больше, чем 104. Теперь нужно вычесть полученный результат (84) из 104 и записать остаток под новой горизонтальной чертой.

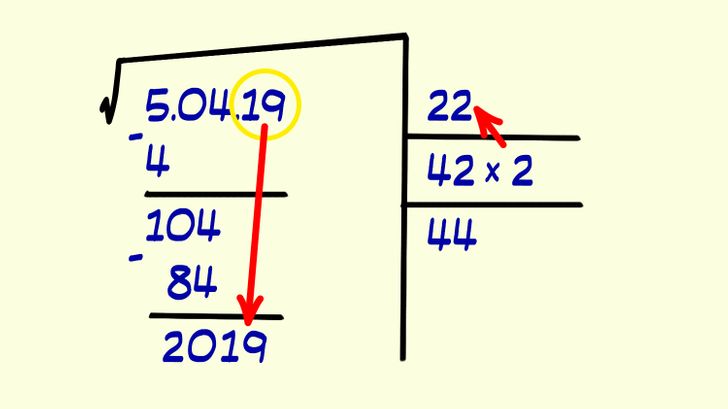
5. Снесите оставшиеся цифры подкоренного числа. Запишите найденное вами на прошлом шаге число (2) в строку результата, в результате чего теперь там будет число 22.

Как и раньше, число из строки результата умножаете на 2, получаете в данном случае 44 и записываете во вспомогательной строке.

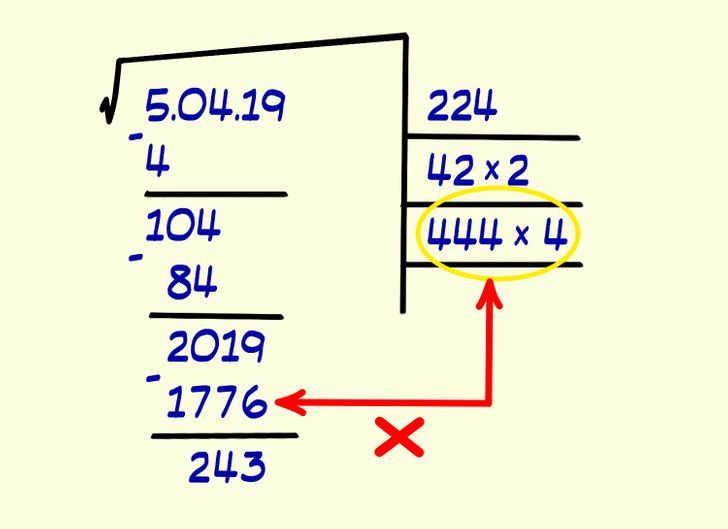
6. Снова найдите такое целое число, чтобы после добавления его в выражение 44_ × _ у вас в результате получилось число, равное или максимально приближенное к числу 2 019 (но не большее). В нашем примере лучше всего подойдет четверка, так как 444 × 4 = 1 776. Число 1 776 меньше числа 2 019 (если бы мы взяли 5 и подставили ее в выражение, то получили бы в результате число 2 225, которое больше, чем 2 019). Запишите подобранное вами число (4) в строку результата.

Теперь полученный результат (1 776) необходимо вычесть из числа 2 019 и записать остаток (243) под новой горизонтальной чертой. Наличие остатка говорит о то, что мы еще не вычислили точный квадратный корень. Как продолжить вычисления, если в подкоренном числе закончились цифры для переноса? Это означает, что квадратным корнем является не целое число, а десятичная дробь. Для продолжения расчетов к остатку переносим два нуля и повторяем действия так, как делали выше.

Умножаем 224 на 2, результат записываем на вспомогательной линии. Подбираем число к выражению 448_×_, чтобы результат был равным или максимально приближенным к числу 24 300. В этом нам поможет пятерка, благодаря которой получаем число 22 425. Пятерку записываем в поле результата после запятой. Снова получаем остаток, снова переносим два нуля и продолжаем расчет.

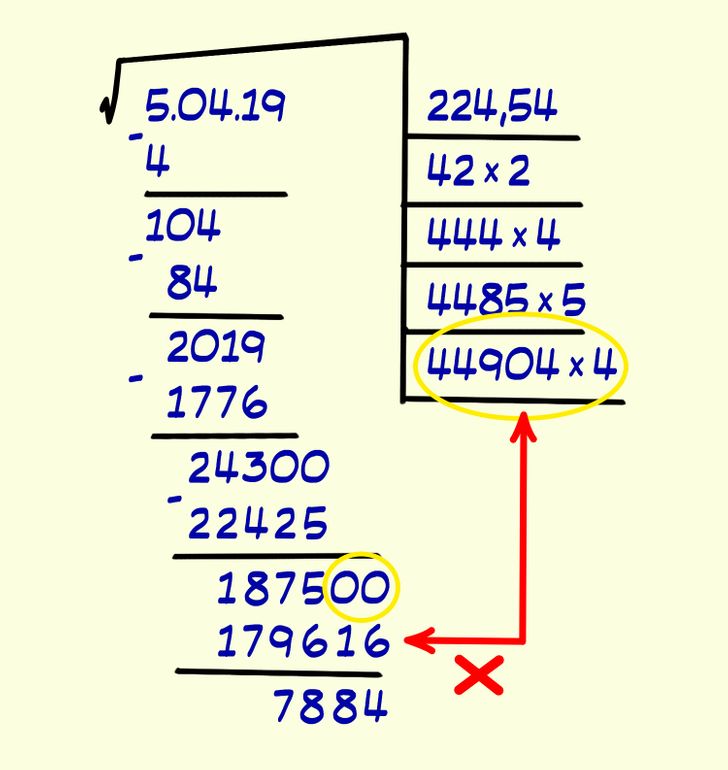
Выше не картинке представлены дальнейшие действия, но нет окончательного ответа. Таким образом можно продолжать вычислять точный корень, пока в остатке не появится ноль. Но нужно понимать, что не всегда корень можно извлечь.

На первый взгляд кажется, что данный метод сложный и долгий, но многое зависит от конкретного числа и, соответственно, его корня. Например, попробуйте указанным выше способом вычислить корень из числа 2 116. На это уйдет меньше минуты и займет всего пару действий.