Отрицательные числа, их свойства и выражения с ними

Когда мы считаем что-то, то пользуемся натуральными числами. Например, сначала отрезаем от торта один кусок, затем другой и получаем уже 2 маленьких куска торта. Или собираем в саду яблоки, срывая одно яблоко, затем еще одно, и уже имеем 2 яблока. При этом мы прибавляем одно число к другому, то есть пользуемся сложением. Если же аналогичным образом использовать вычитание, то в определенный момент мы столкнемся со множеством отрицательных чисел.

«Бери и Делай» объясняет, что такое отрицательные числа, какими отличительными свойствами они обладают и о чем полезно знать при работе с ними.

Что такое отрицательное число

На первый взгляд кажется, что отрицательные числа вряд ли нужны нам в жизни. Но зайдите в лифт крупного торгового центра, и вы наверняка увидите там этажи с парковками, которые чаще всего располагаются под землей и обозначаются как «−1-й этаж», «−2-й этаж» и так далее.

Отрицательные числа есть и на уличном градуснике: когда за окном холодно и вода замерзает, превращаясь в лед, столбик термометра опускается ниже нулевой отметки, показывая, что на улице минусовая температура.

Из этого можно сделать вывод, что отрицательные числа начинаются за нулевой чертой. Для лучшего понимания нарисуем числовую прямую.

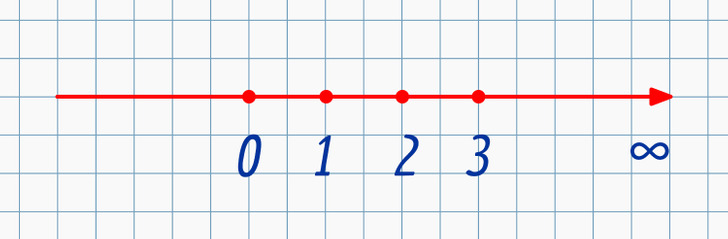
На листе бумаги в клетку нарисуйте линию. На ней поставьте точку отсчета, обозначающую 0. Теперь отступите от нее вправо на 1 см (2 клетки) и сделайте еще одну отметку. Подпишите ее как число 1. Аналогичным образом справа можно расположить остальные числа по порядку вплоть до бесконечности. Значения всех этих чисел больше 0, и их называют положительными числами. Иногда рядом с такими числами ставят плюс, поэтому +1 = 1, а 1 = +1.

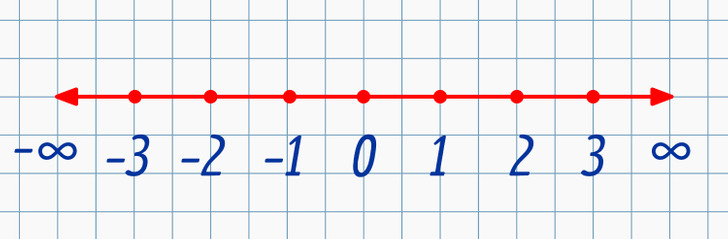
Если двигаться в левую сторону, то мы обнаружим числа, чье значение меньше 0. Поэтому их называют отрицательными числами и ставят рядом с ними минус. При этом −1 не равняется 1. Отрицательные числа располагаются симметрично по отношению к положительным числам, а ноль не относится ни к одним, ни к другим.

Если ноль — это ничто, как может быть что-то меньшее, чем ничто? Ноль — это еще и точка отсчета, которая разделяет числа на числовой прямой. При этом добавление отрицательных чисел расширяет возможности счета. Представим, что на банковской карте было 100 рублей. После похода в магазин ее баланс стал равняться −100 рублям. Сколько денег нужно положить на счет карты, чтобы ее баланс снова стал положительным и равнялся 100 рублям? Если добавить только 100 рублей, то мы избавимся от отрицательного числа и баланс будет равен 0. Если добавить еще 100 рублей, то баланс вновь станет положительным и будет равен +100 рублям.

Это все станет ясно, если вы посмотрите на числовую прямую. Для каждого натурального числа существует одно и только одно отрицательное число, которое дополняет его до 0. Если к числу −100 прибавить 100, то получится 0. Если к 100 прибавить −100, то результат будет аналогичным. Из этого можно сделать следующие выводы:

• (−a) + (+a) = 0
• (−a) + 0 = (−a)
• − (−a) = a

Как сравнивать отрицательные числа

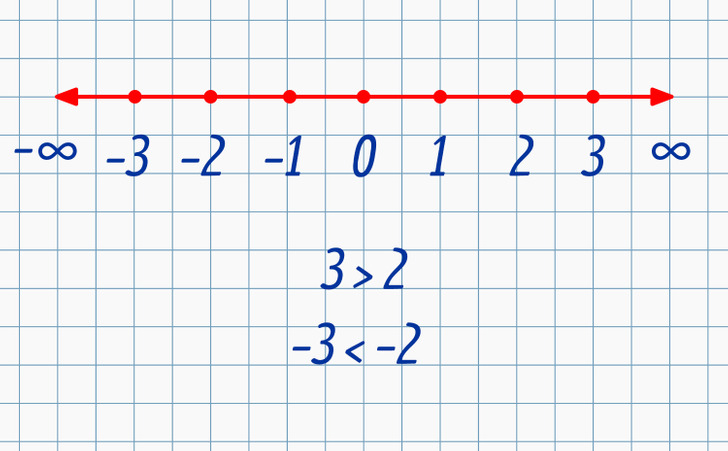
Все отрицательные числа, как и положительные, располагаются на числовой прямой в определенном порядке. Это позволяет сравнивать их между собой. Но есть определенные особенности: одно положительное число больше другого, если оно фактически располагается от него дальше в правую сторону. Другими словами, число 3 больше 2, потому что находится правее. С отрицательными числами все немного иначе: число −3 меньше −2, потому что находится левее на числовой прямой.

Арифметические действия с отрицательными числами

Знак, стоящий перед числом, необходимо учитывать, так как от этого зависит результат.

• При сложении 2 положительных чисел в результате всегда получается положительное число. Пример: 2 + 3 = 5.
• При сложении 2 отрицательных чисел в результате всегда получается отрицательное число. Пример: (−2) + (−3) = (−5). Чтобы понять, почему так происходит, вспомните числовую прямую: если к −2 мы добавим еще −3, то уйдем еще левее до −5.

• При сложении положительного и отрицательного чисел, если положительное число представляет собой число с большей абсолютной величиной, результатом будет положительное число. Пример: 5 + (−3) = 2. Фактически из 5 мы вычитаем 3, поэтому в результате получаем 2.
• При сложении положительного и отрицательного чисел, если отрицательное число представляет собой число с большей абсолютной величиной, результатом будет отрицательное число. Пример: 5 + (−10) = (−5). Фактически мы прибавляем к −10 число 5, поэтому в результате получаем −5.

Совет: Возможно, вам будет легче, если вы вспомните правила расстановки знаков после снятия скобок. Например, (+5) + (−3) = 5 − 3 = 2. Или (+5) + (−10) = 5 − 10 = (−5).

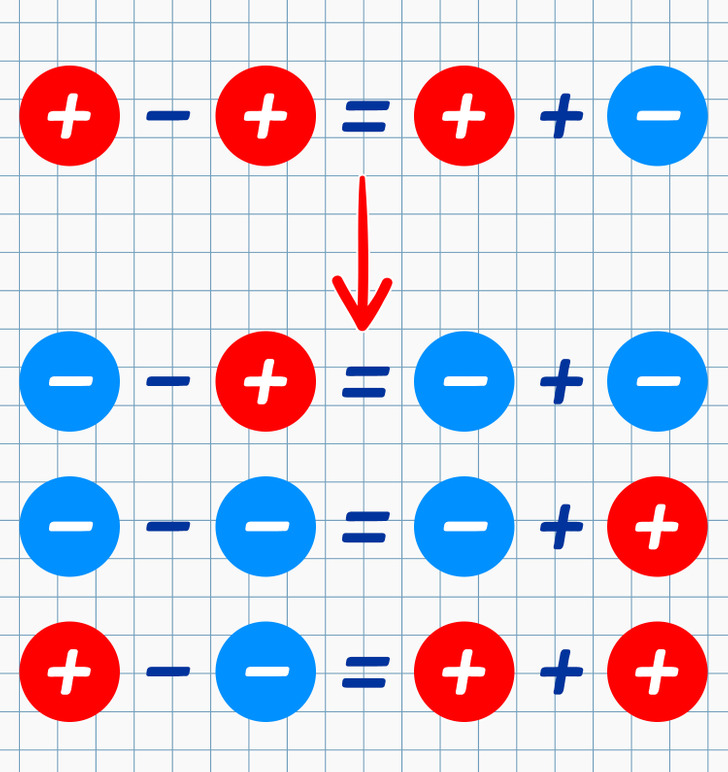
• Так как вычитание — это действие, противоположное сложению, то тогда, чтобы из одного числа вычесть другое, нужно к уменьшаемому прибавить число, противоположное вычитаемому. Пример: (−2) − (+5) = (−2) + (−5) = (−7). Или 5 − (−2) = 5 + (+2) = 7.

Где на практике с этим можно столкнуться? Представьте, что на улице была температура −2 °C, а сейчас она понизилась еще на 10 °C. Какая температура теперь на улице? Фактически вам нужно из −2 вычесть 10 или к −2 прибавить −10. И тогда в результате получится −12 °C.

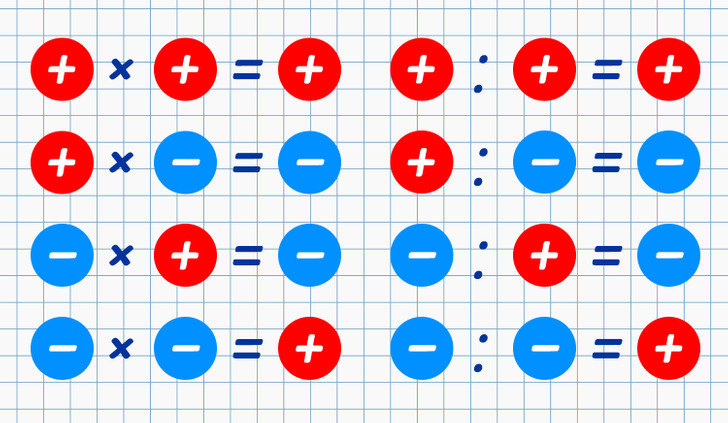
• При умножении и делении чисел действует правило знаков: произведение или частное чисел с разными знаками отрицательно, а с одинаковыми — положительно. При этом в делении и умножении участвуют фактически модули чисел. Другими словами, (−а) × (−b) = a × b.

Где на практике можно с этим столкнуться? К примеру, муж и жена залезли в долги. У каждого по 100 рублей долга. Чему равен их общий долг? Для этого нужно сложить оба долга: (−100) + (−100). Или же можно просто умножить 1 долг на 2: (−100) × 2. В результате получается −200 рублей. Так как речь идет о долге, то перед числом в результате стоит минус.

• Если нужно возвести число в отрицательную степень, «переверните» выражение, записав его в виде дроби с единицей в числителе и с исходным числом в степени в знаменателе. Саму степень замените на положительную, после чего возведите число в положительную степень. Пример: a⁻ⁿ = 1/aⁿ.